【2024年 数学】香川県公立高校入試 過去問解説
香川県公立高校入試
2024年(令和6年) 数学
過去問解説
※当サイトの内容、テキスト、画像等の無断転載・無断使用を固く禁じます。
問題1
(1) \( 7\times (-2)-(-5) \)
\( -14 + 5 =-9\)
解答. -9
・四則演算は①「×、÷」②「+、-」の順に計算
(今回は\( 7\times (-2) \)の計算を最初に行う)
・マイナスを含む計算は符号に注意!
\( 7\times (-2)={\color{red}-}14 \)、\( -(-5)={\color{red}+}5 \)
(2) \( a=-3 \) を \( a^2 +\displaystyle\frac{ 15}{ a } \)に代入
\( (-3)^2 + \displaystyle\frac{\cancelto{\color{red}5}{15}}{ -\cancelto{\color{red}1}{3}}=9-5=4\)
解答. 4
・負の数の累乗計算はかっこの有無に注意!
例)
\((-3)^2=(-3)\times(-3)=+9\)
\(-3^2=-(3\times3)=-9\)
(3) \( 4a^3b^2 \div\displaystyle\frac{ 1}{ 2 }ab=4a^3b^2 \div\displaystyle\frac{ ab}{ 2 }\)
と式変形できる。逆数に直して計算すると
\( 4a^{\cancelto{\color{red}2}{3}}b^{\cancelto{\color{red}1}{2}} \times \displaystyle\frac{2}{\cancel{ab}}=4a^2b\times2=8a^2b\)
解答. \(8a^2b\)

分母と分子を明確にしてから逆数に式変形するとミスを防げるよ!
・分母と分子を明確にしてから逆数に式変形!
・約分後の数字はしっかり明記!
(4)\(\cases{3x + 5y= 4\cdots①\\x-y= 4\cdots②}\)
\(xまたはy\)の係数をそろえて加減し、\(1\)文字消去
加減法で解く場合、符号が異なる方の係数(今回は\(y\))をそろえて加法で解く方がミスが少ない



\(x\)の係数をそろえる場合、減法を用いるのでミスが起きやすいね
今回は符号が異なる\(y\)を消去したいので、②を\(5\)倍して\(①+(②\times5)\)を計算する
<②を\(5\)倍>
\(5x -5y= 20\)
\(\Longrightarrow\)
<\(①+(②\times5)\)>
\(\cases{3x + 5y= 4\\5x -5y= 20}\)
<②を\(5\)倍>
\(5x -5y= 20\)
<\(①+(②\times5)\)>
\(\cases{3x + 5y= 4\\5x -5y= 20}\)
計算すると \(\begin{align}8x&=24\\x&=3\end{align}\)
①または②の式に\(x=3\)を代入(今回は②(\(x-y= 4\))に代入)
\(\begin{align}3-y&=4\\-y&=4-3\\-y&=1\\y&=-1\end{align}\)
解答. \(x=3, y=-1\)



他の解き方はありますか?



他に「代入法」で解く方法もあるよ!
「\(x=\)~」または「\(y=\)~」の式に変形し、もう一方の式に代入
②の式を変形して\(x=4+y\cdots②’\)にする
①\(3x + 5y= 4\)の\(x\)に\((4+y)\)を代入
\(\begin{align}3(4+y)+5y&=4\\12+3y+5y&=4\\12+8y&=4\\8y&=4-12\\8y&=-8\\y&=-1\end{align}\)
\(②’x=4+y\)に\(y\)の値を代入して\(x\)を求める
\(\begin{align}x&=4+(-1)\\x&=4-1\\x&=3\end{align}\)



式によっては代入法の方が簡単な場合もあるので両方知っておこう!



今回の場合は②の式の\(x,y\)の係数がどちらも\(1\)なので、代入法でも良さそう!



その通り!代入法は\(x,y\)の係数が\(1\)のときに有効なので試してみてね!
・\(x,y\)のうち、符号の異なる方の係数をそろえる
・符号が同じのときは、係数の小さいものに合わせる
・方程式どうしの引き算は符号間違いに注意
・\(x,y\)の係数が\(1\)のときは代入法
(5)\(\sqrt{50}-\sqrt{2} + \displaystyle\frac{6}{\sqrt{2}}\)



ルートの計算は中身を簡単にしたり有理化してから解きましょう!
<ルートの中身を簡単にする方法>
- ルートの中を素因数分解する
- 同じ数字がある場合は\(2\)個\(1\)セットでルートの外に出す
\(\sqrt{50}\rightarrow\sqrt{2\times{\color{red}5}\times{\color{red}5}}\rightarrow5\sqrt{2}\)
<有理化とは?>
⇒分母にルートが含まれない形に変換すること
- 分母にあるルートと同じものを分母分子両方にかける
- 分母分子で約分できる場合は約分する
\(\displaystyle\frac{6}{\sqrt{2}}\rightarrow\displaystyle\frac{6\times{\color{red}\sqrt{2}}}{\sqrt{2}\times{\color{red}\sqrt{2}}}\rightarrow\displaystyle\frac{{\cancelto{\color{red}3}{6}}\sqrt{2}}{{\cancelto{\color{red}1}{2}}}\rightarrow3\sqrt{2}\)
\(\begin{align}&\displaystyle\frac{6}{\sqrt{2}}\rightarrow\displaystyle\frac{6\times{\color{red}\sqrt{2}}}{\sqrt{2}\times{\color{red}\sqrt{2}}}\rightarrow\displaystyle\frac{{\cancelto{\color{red}3}{6}}\sqrt{2}}{{\cancelto{\color{red}1}{2}}}\\&\rightarrow3\sqrt{2}\end{align}\)
よって
\(\begin{align}\sqrt{50}-\sqrt{2} + \displaystyle\frac{6}{\sqrt{2}}&=5\sqrt{2}-\sqrt{2}+3\sqrt{2}\\&=8\sqrt{2}-\sqrt{2}\\&=7\sqrt{2}\end{align}\)
\(\begin{align}&\sqrt{50}-\sqrt{2} + \displaystyle\frac{6}{\sqrt{2}}\\&=5\sqrt{2}-\sqrt{2}+3\sqrt{2}\\&=8\sqrt{2}-\sqrt{2}=7\sqrt{2}\end{align}\)
解答. \(7\sqrt{2}\)
・ルートは中身を簡単にしてから計算
・分母のルートは有理化
(6)\((x+3)^2-(x+3)-30\)を因数分解



難しい計算式で大変そう・・



そのまま解くと難しいから、まずは簡単な式に直せるか考えよう!
よく見ると\((x+3)\)という同じ式が\(2\)回出てきているのでそこを\(1\)つの文字に置き換えてみよう!
\((x+3)=t\)と置くと、
\(t^2-t-30=(t-6)(t+5)\)



よく見る二次方程式の形になって因数分解できました!
①掛け算で30(定数部分)になる2つの整数の組み合わせを考える
今回の場合は(1, 30)(2, 15)(3, 10)(5, 6)の4通り
※実際には\(-30\)なので、どちらかの数字がマイナスになる
②①の中で足し算で\(-1\)(\(t\)の係数)になる組み合わせを選ぶ
今回は\(t\)の係数が\(-1\)なので、2つの数のうち大きい数の方がマイナスになる
今回の場合は\((-6, 5)\)が当てはまる
因数分解した式に\(t=x+3\)を代入
\(\begin{align}(t-6)(t+5)&=(x+3-6)(x+3+5)\\&=(x-3)(x+8)\end{align}\)
\(\begin{align}&(t-6)(t+5)\\&=(x+3-6)(x+3+5)\\&=(x-3)(x+8)\end{align}\)
解答. \((x-3)(x+8)\)



最後に\(t=x+3\)を代入するのを忘れずにね!
・同じ式は\(1\)つの文字に置き換えて簡単な式にする
(今回の場合は\(t=x+3\))
・置き換えた文字の戻し忘れに注意!
(7)㋐\(-\sqrt{11}\) ㋑\(3\) ㋒\(-4\)
㋑のみ正の数なので1番大きいのは㋑\(3\)
次に㋐と㋒で大きさを比較していく



ルートと整数の比較はどちらかに統一して大きさを比べよう!
- 整数をルートにして比較
- ルートを整数にして比較
整数をルートに変換して大小を確認
\(-4=-\sqrt{4^2}=-\sqrt{16}\)
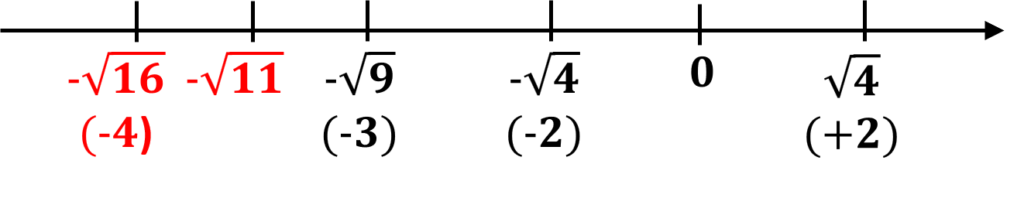
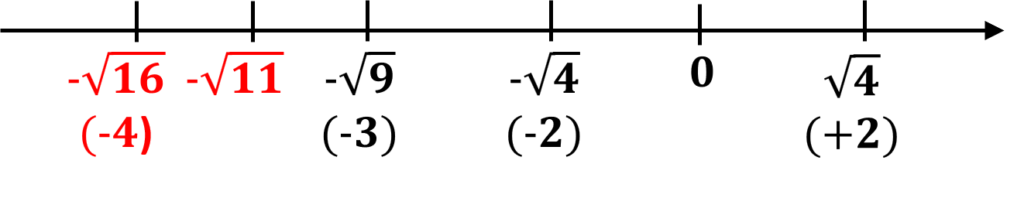
ルートは二乗した数同士で挟んでおおよその数を確認
\(\begin{align}3^2 < 11 < 4^2\\3 < \sqrt{11} < 4\\\sqrt{11}=3.\cdots\end{align}\)





数直線上で確認すると負の数の場合も比較しやすいよ!
よって
\(-4<-\sqrt{11}\)
であることがわかる
解答. ㋒⇒㋐⇒㋑
・ルートと整数の比較はどちらかに統一して比較する
・負の数は絶対値が大きい方が値としては小さくなるので注意!(例:\(-100 < -1\))
問題2
(1)
\(\angle{CED}\)を求める問題
・\(ABCD\)は平行四辺形
・直線\(BC\)上に\(BD = BE\) となる点Eを取っている
①求めたい部分から何が必要か、何が使えるか考える
②必要な部分を図形の性質を利用して求めていく
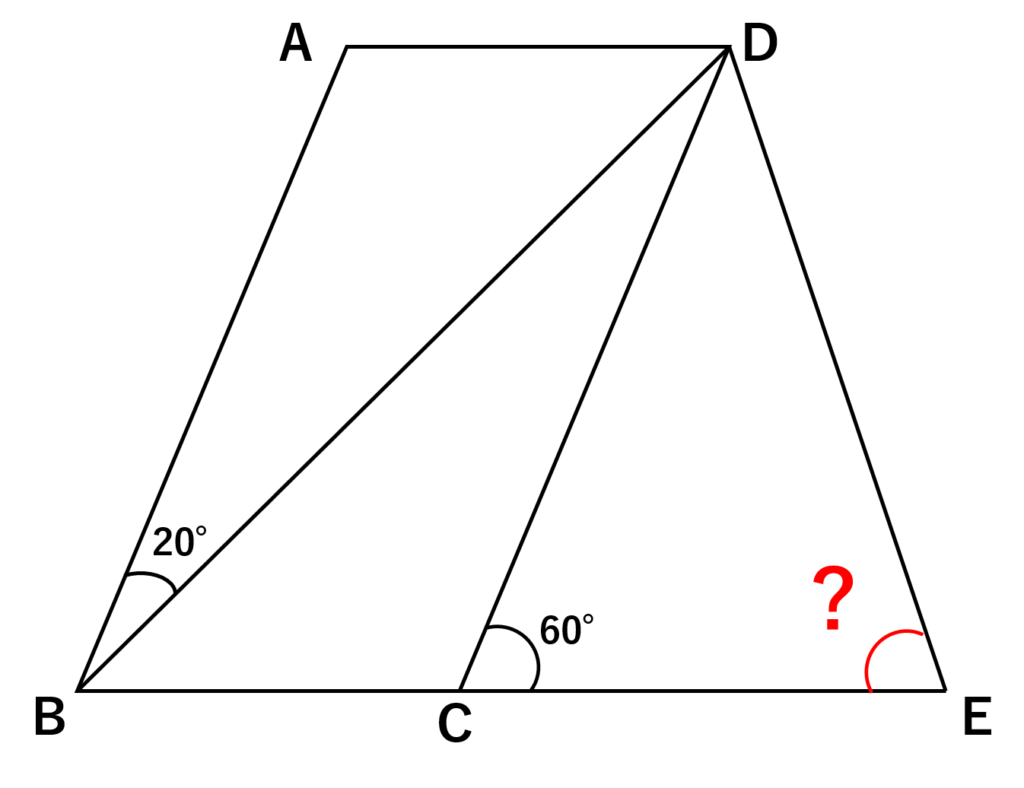
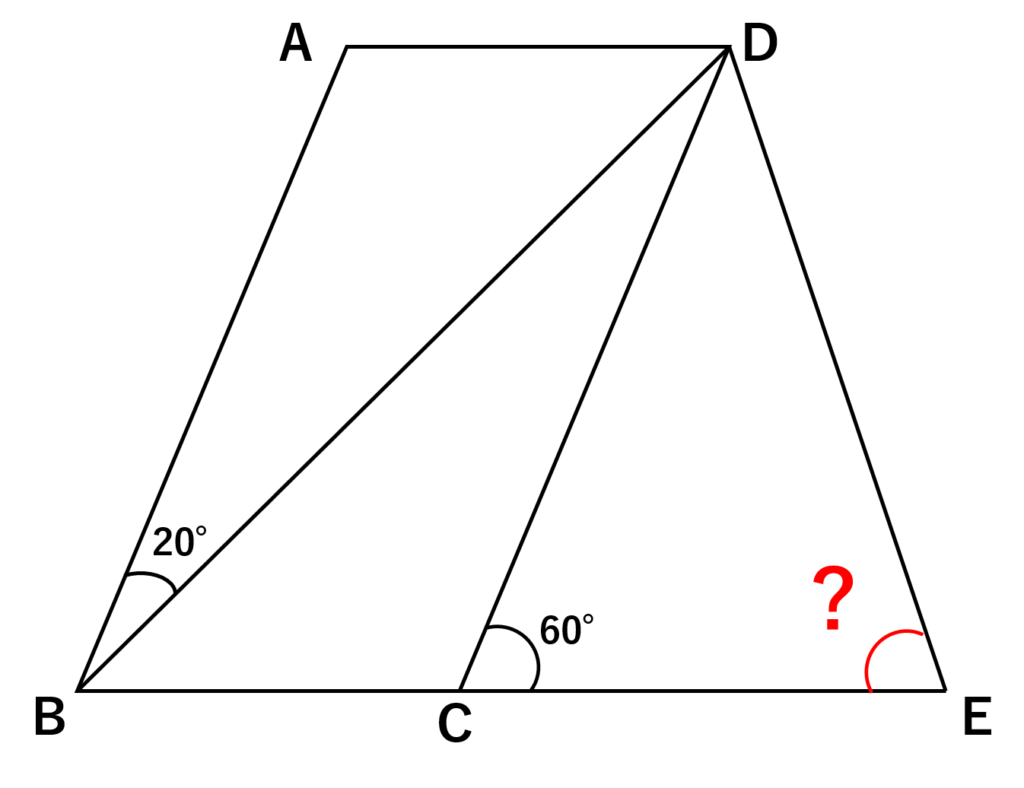
問題文より\(BD = BE\)なので\(\triangle BDE\)は二等辺三角形ということがわかる
つまり\(\angle{BDE}=\angle{BED}\)
\(\rightarrow\angle{DBE}\)がわかれば\(\angle{BED}(=\angle{CED})\)が求められる
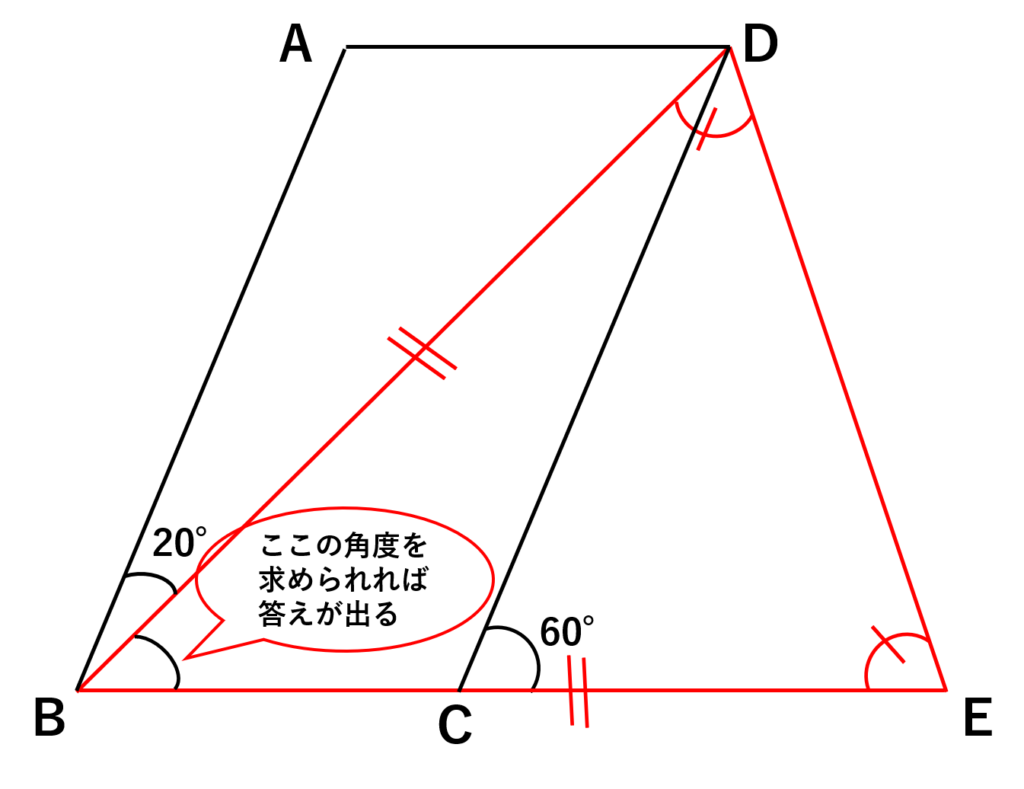
\(\triangle BDE\)は二等辺三角形より
\(\angle{BED}=\displaystyle\frac{180\text{°}-{\angle{DBE}}}{2}\)

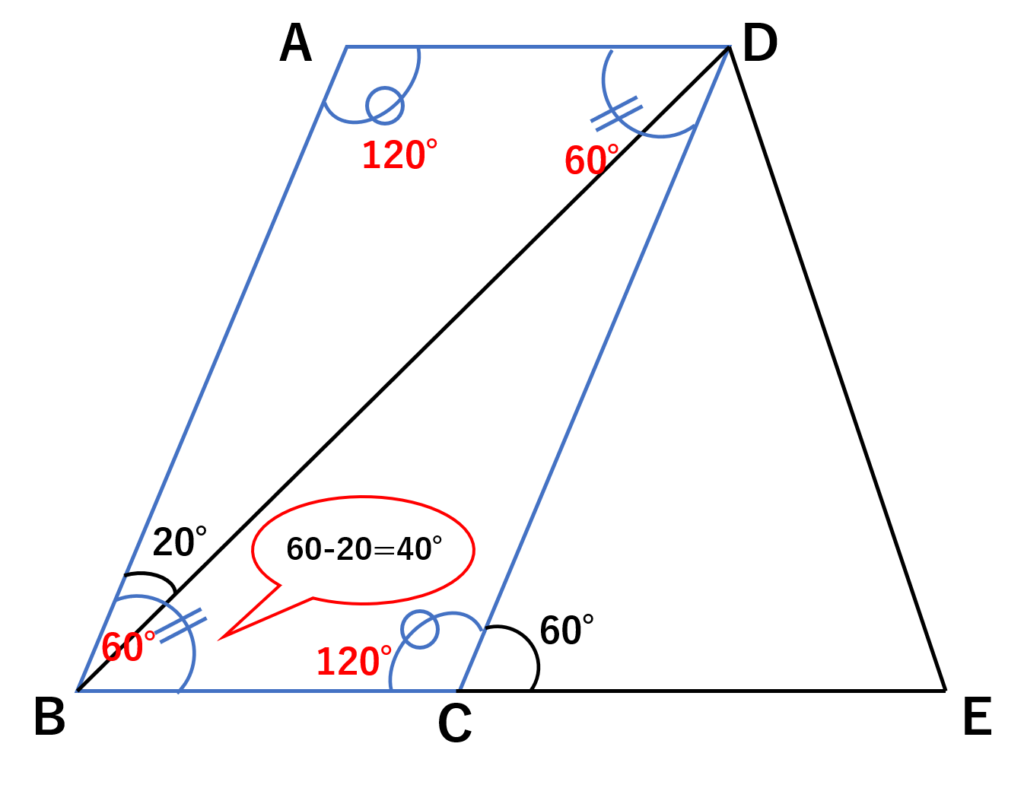
平行四辺形\(ABCD\)に注目すると
\(\angle{BCD}=180\text{°}-60\text{°}=120\text{°}\)
平行四辺形は向かい合う角が等しいので
\(\angle{BCD}=\angle{BAD}=120\text{°}\)
\(\begin{align}\angle{BCD}+\angle{BAD}&=120\text{°}\times2\\&=240\text{°}\end{align}\)
\(\begin{align}\angle{ABC}+\angle{ADC}&=360\text{°}-240\text{°}\\&=120\text{°}\end{align}\)
\(\begin{align}&\angle{ABC}+\angle{ADC}\\&=360\text{°}-240\text{°}=120\text{°}\end{align}\)
\(\angle{ABC}=\angle{ADC}\)なので
\(\angle{ABC}=120\text{°}\div2=60\text{°}\)
\(\angle{DBC}=60\text{°}-20\text{°}=40\text{°}\)



\(\angle{BED}\)は二等辺三角形\(\triangle BDE\)の性質より、
\(\begin{align}\angle{BED}&=\displaystyle\frac{180\text{°}-{\angle{DBE}}}{2}\\&=\frac{180\text{°}-40\text{°}}{2}\\&=\frac{140\text{°}}{2}=70\text{°}\end{align}\)
\(\angle{BED}=\angle{CED}\)なので
\(\angle{CED}=70\text{°}\)
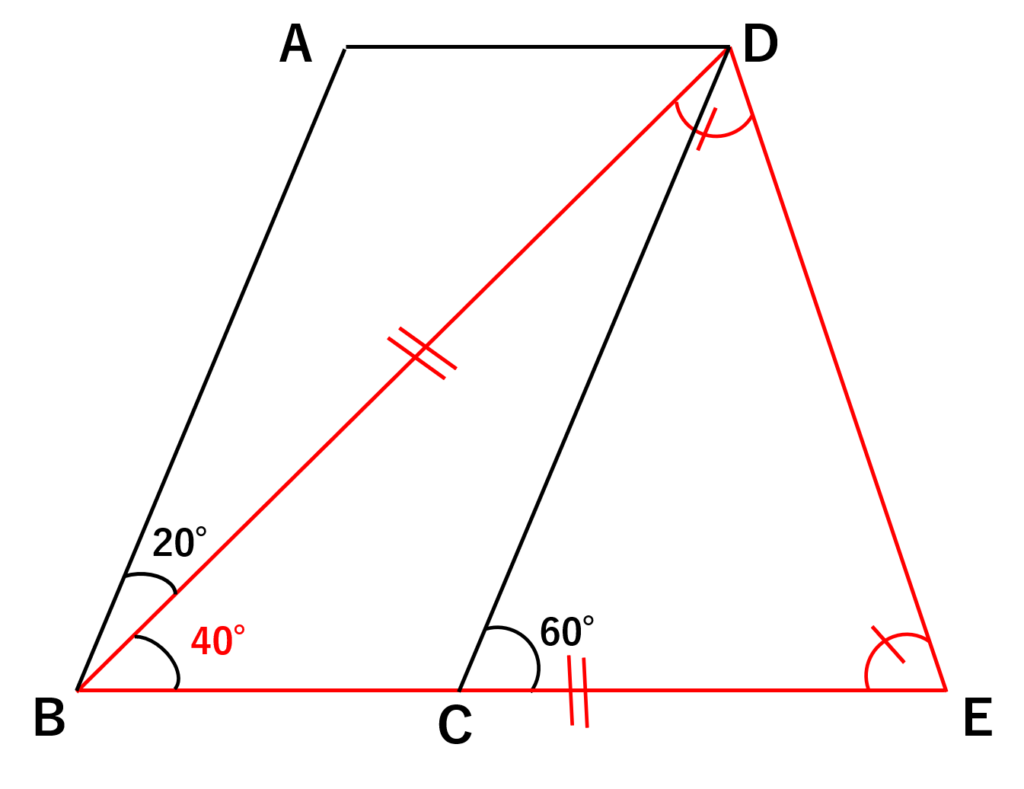

解答. \(\angle{CED}=70\text{°}\)
(2)
ア 線分DFの長さを求める
・\(ABCD\)は長方形⇒四角は全て直角
・\(EF\)と対角線\(BD\) の交点を\(G\)とする


・\(DF\)を求めるためにどの三角形を利用するのが良いか考える
・\(\triangle CDF\)を使えば三平方の定理で計算できる
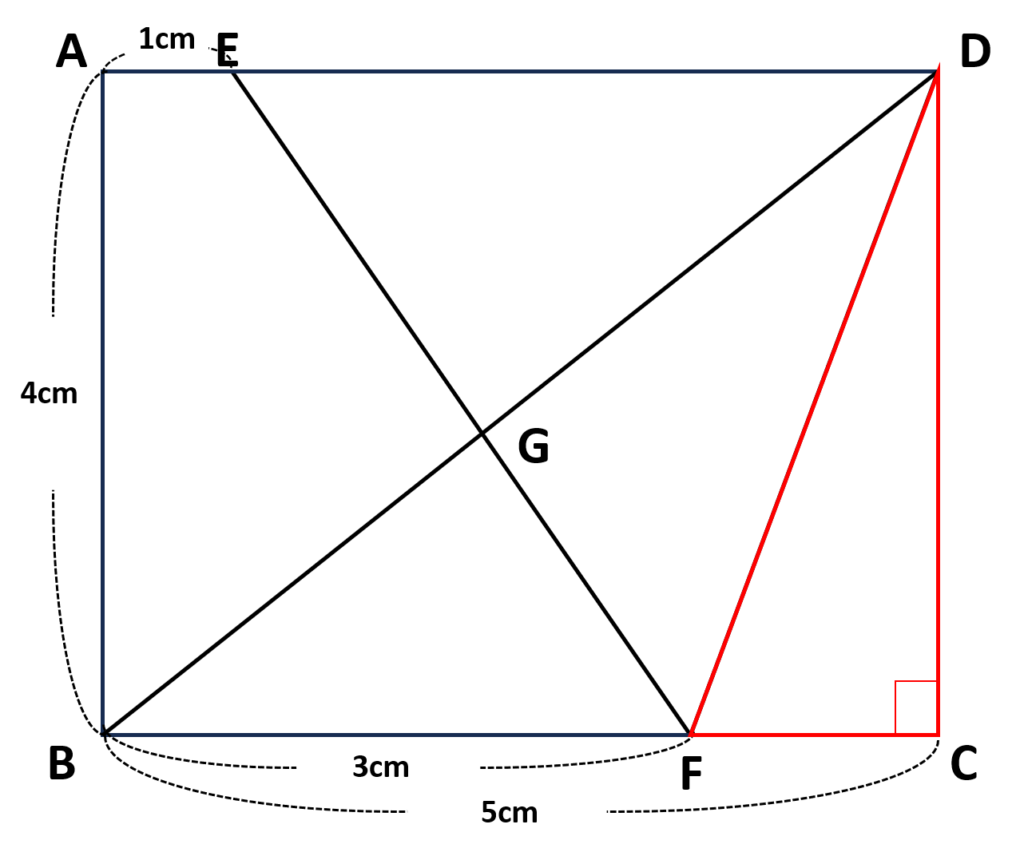

・\(CF=BC-BF=5-3=2cm\)
・\(CD=4cm\)
三平方の定理より
\((DF)^2=(CF)^2+(CD)^2\)
\(\begin{align}(DF)^2&=(2)^2+(4)^2\\&=4+16\\&=20\\\end{align}\)
よって
\(DF=2\sqrt{5}\)
解答. \(DF=2\sqrt{5}cm\)
イ 四角形\(ABGE\)の面積を求める
・四角形\(ABGE\)の面積を直接求めるのは難しそう
・全体から不要な部分を引く、または四角形\(ABGE\)を分割して求める方法を考えていく


今回は2つの解法パターンを説明します
《1. 四角形\(ABFE-\triangle BFG\)で求める》
四角形\(ABFE\)は今ある情報で出せる
⇒①\(\triangle BFG\)の面積がわかれば求められる
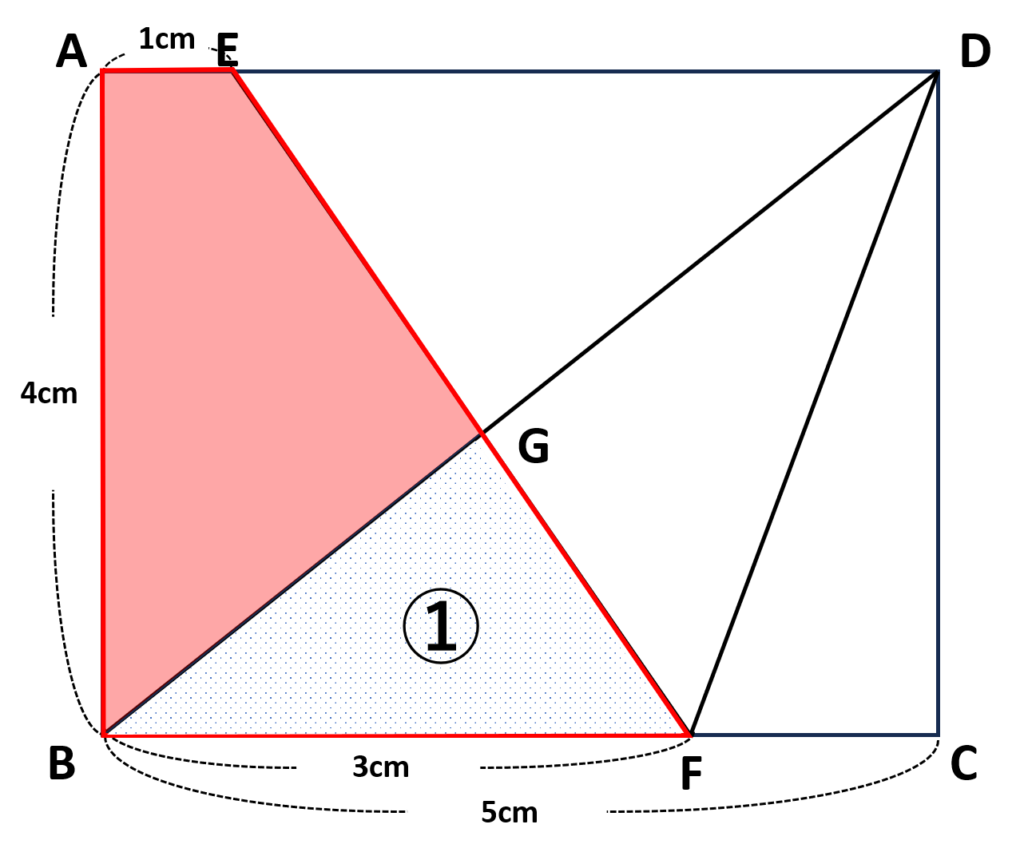

四角形\(ABFE\)は台形なので台形の面積の公式を用いる
\((上底+下底)\times高さ\times\displaystyle\frac{1}{2}\)
\(\begin{align}四角形ABFE&=(1+3)\times4\times\displaystyle\frac{1}{2}\\&=4\times\cancelto{\color{red}2}{4}\times\displaystyle\frac{1}{\cancelto{\color{red}1}{2}}=8\end{align}\)

あとは①\(\triangle BFG\)を求めていく
⇒\(\triangle BFG\)の高さがわかれば面積は出せる


\(\triangle BFG\)と関連のありそうな図形をみていくと\(\triangle DEG\)が\(\triangle BFG\)と相似であることがわかる
・対頂角より\(\angle{BGF}=\angle{DGE}\)
・長方形は向かい合う辺が平行なので、錯角より\(\angle{GBF}=\angle{GDE}\)
(\(\angle{GFB}=\angle{GED}\)でも良い)
よって\(\triangle BFG\unicode[sans-serif]{x223D}\triangle DEG\)

相似より\(BF:DE=BG:DG=3:4\)
この辺の比を用いて\(\triangle BFG\)の高さを出したい
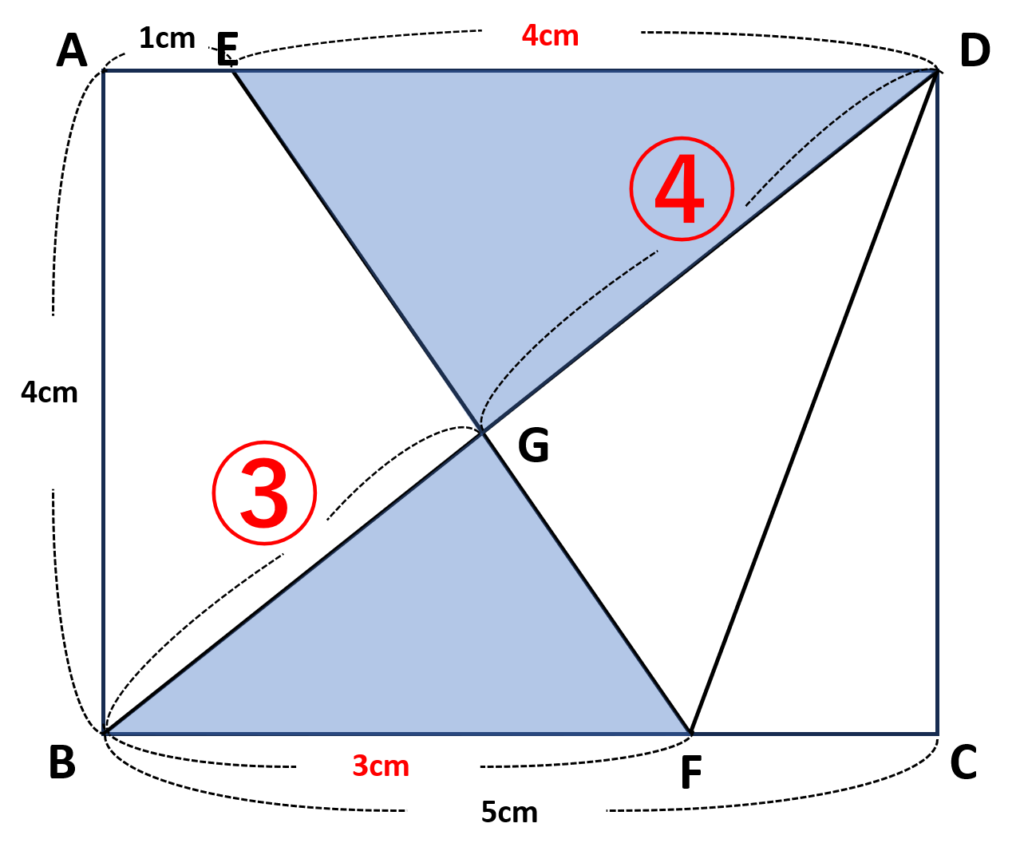

そこで\(G\)から辺\(BC\)に垂線を下ろし、辺\(BC\)との交点を\(H\)とおく
すると、\(\triangle BHGと\triangle BCD\)が相似であることがわかるので、先ほどの辺の比を用いて\(GH\)を求めていく
・\(\angle{B}\)は共通
・\(\angle{BHG}=\angle{BCD}=90\text{°}\)
よって\(\triangle BHG\unicode[sans-serif]{x223D}\triangle BCD\)
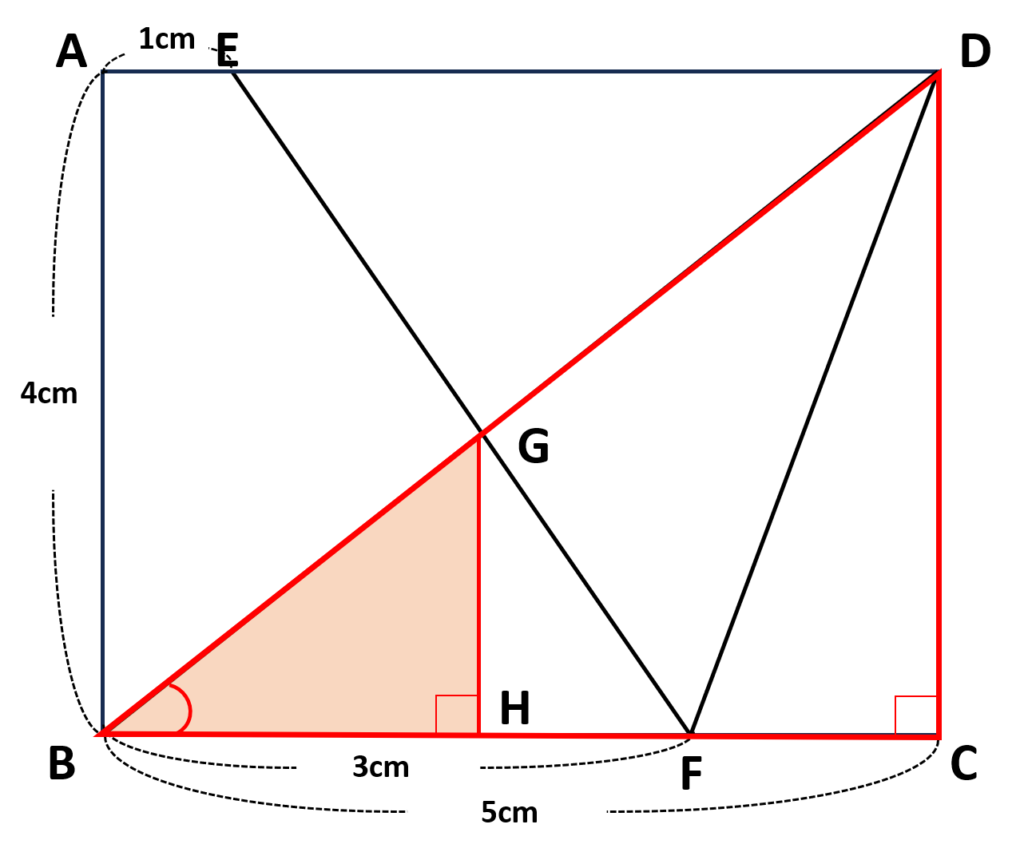

\(BG:GD=3:4\)より\(BG:BD=3:(3+4)=3:7\)
\(\triangle BHG\)と\(\triangle BCD\)の辺の比は\(3:7\)なので
\(\begin{align}GH:DC&=3:7\\GH:4&=3:7\\GH\times7&=4\times3\\GH&=\displaystyle\frac{4\times3}{7}\\GH&=\displaystyle\frac{12}{7}\end{align}\)
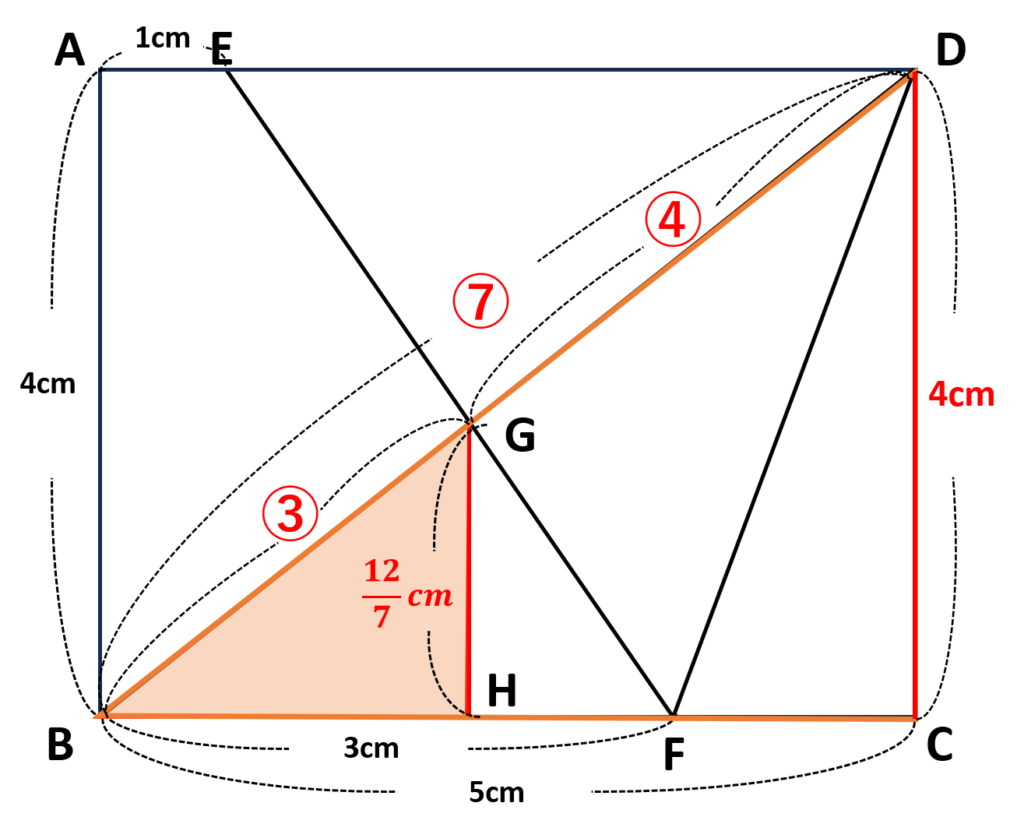

\(GH\)の長さがわかったので、\(\triangle BFG\)の面積を求めていく
\(\begin{align}\triangle BFG&=3\times\displaystyle\frac{\cancelto{\color{red}6}{12}}{7}\times\displaystyle\frac{1}{\cancelto{\color{red}1}2}\\&=\displaystyle\frac{18}{7}\end{align}\)


よって四角形\(ABGE\)の面積は
\(\begin{align}四角形ABFE-\triangle BFG&=8-\displaystyle\frac{18}{7}\\&=\displaystyle\frac{56}{7}-\displaystyle\frac{18}{7}\\&=\displaystyle\frac{38}{7}\end{align}\)
解答. \(\displaystyle\frac{38}{7}cm^2\)
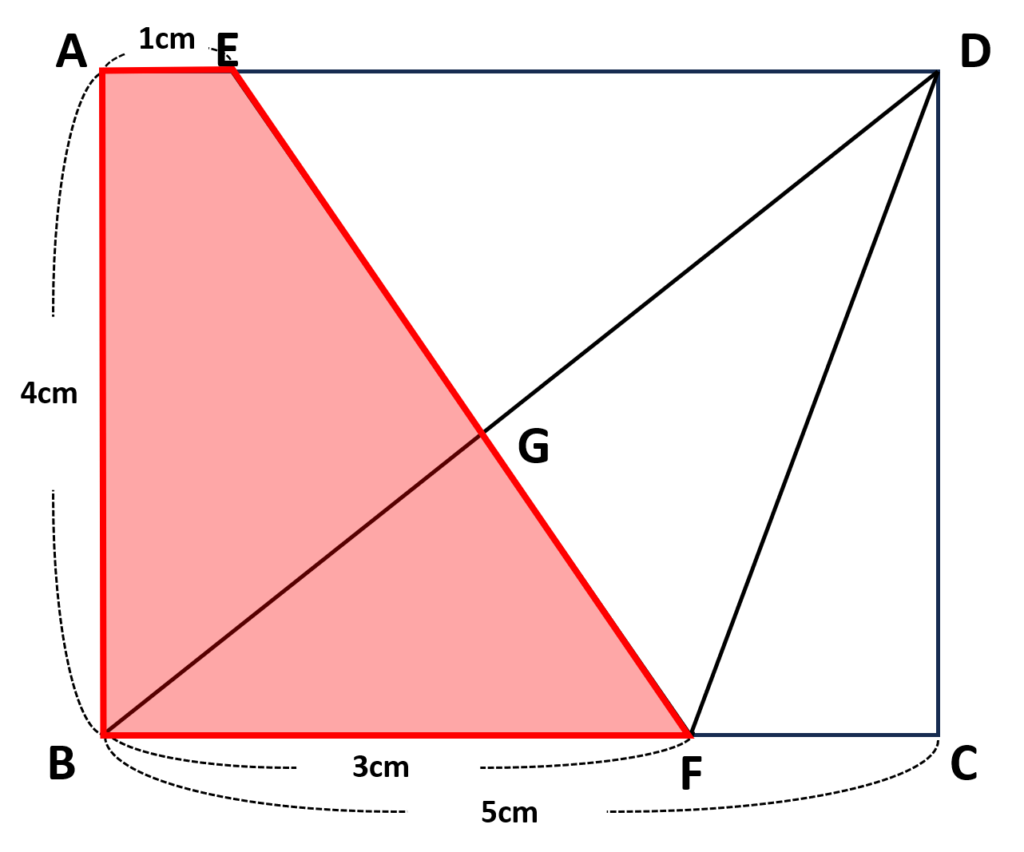
《2. \(四角形 ABCD\)から\(\triangle BCD\)と\(\triangle DEG\)の面積を引く》
この解法では全体の長方形から不要な三角形を引くことで四角形\(ABGE\)の面積を求めていく考え方です
- 1番大きな\(\triangle BCD\)の面積を引く
- \(\triangle DEG\)の面積を求める
\(\triangle DEG\)の面積をどのようにしたら求めることができるかがポイント
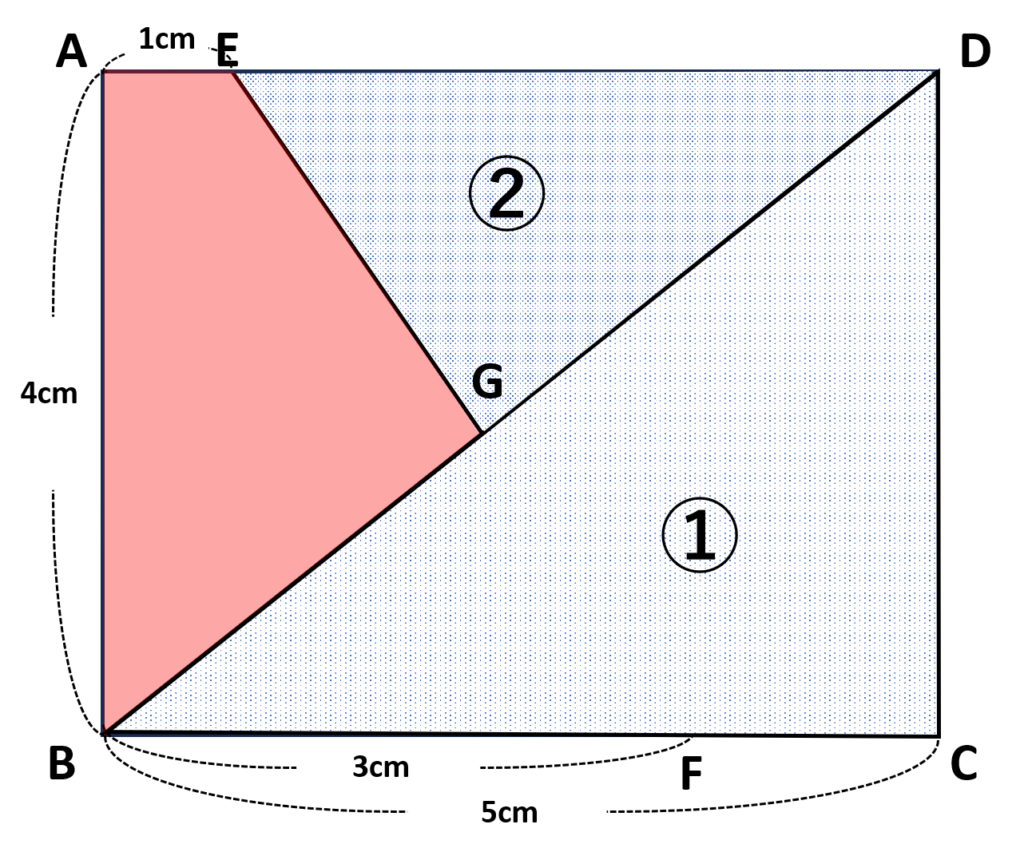

①\(\triangle BCD\)の面積は
\(\triangle BCD=5\times\cancelto{\color{red}2}{4}\times\displaystyle\frac{1}{\cancelto{\color{red}1}{2}}=10\)
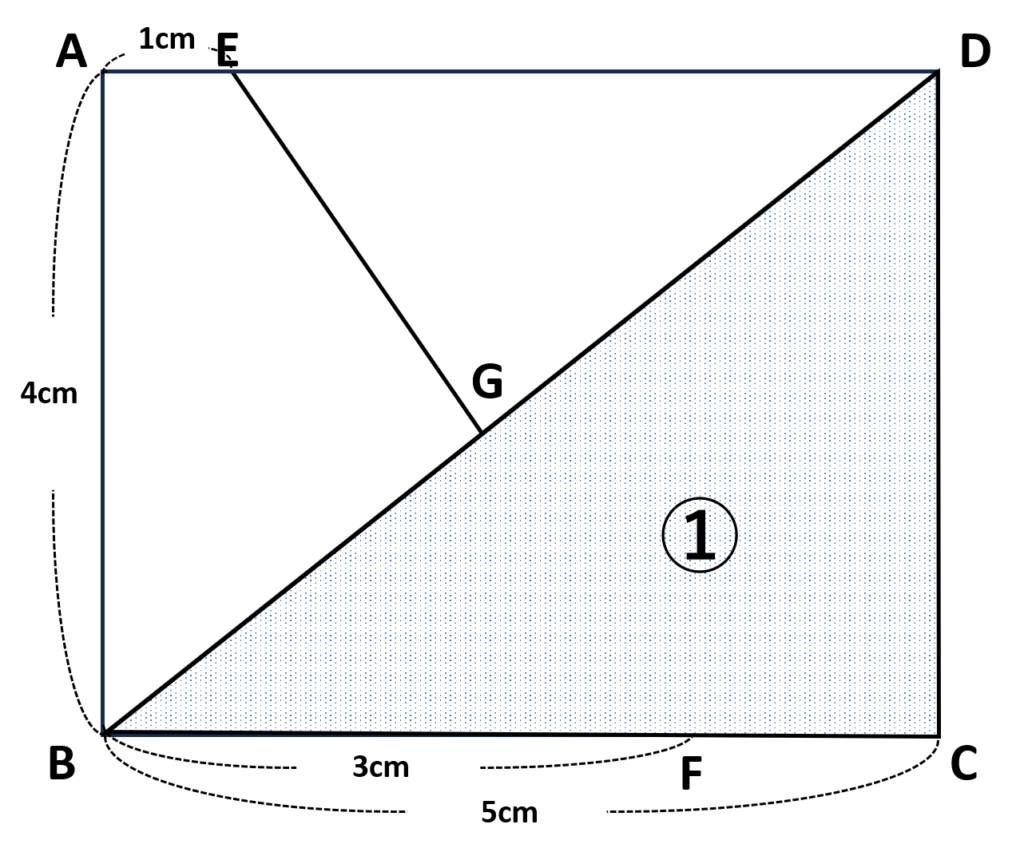

②\(\triangle DEG\)の面積を求めるために\(G\)から辺\(ED\)に垂線を下ろす
辺\(ED\)と垂線との交点を点\(P\)とおく
\(PG\)の長さがわかれば\(\triangle DEG\)の面積が出せる
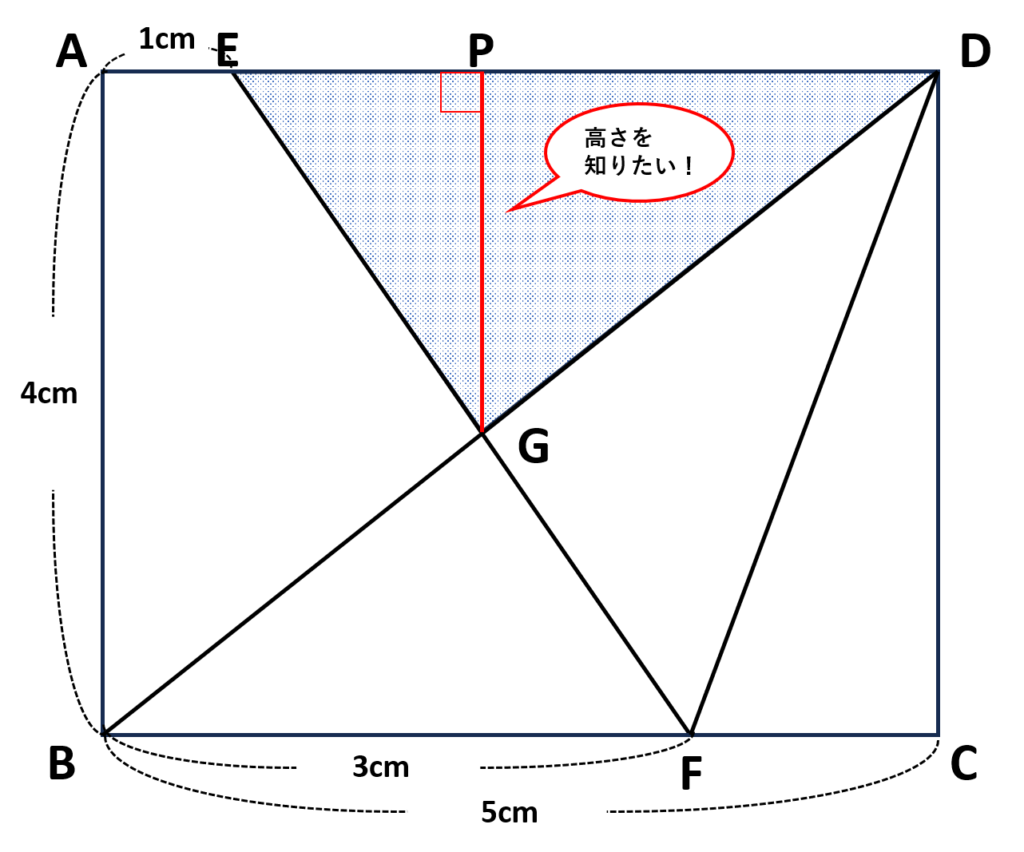

解法①でも利用した\(\triangle BFG\)と\(\triangle DEG\)の相似を利用する
(\(\triangle BFG\)と\(\triangle DEG\)の相似については解法①で説明しているので省略)
\(BF:ED=3:4\)より面積比は
\(\triangle BFG:\triangle DEG=3^2:4^2=9:16\)
相似比が\(a:b\)のとき、面積比は\(a^2:b^2\)


点\(G\)より辺\(BF\)に垂線を下ろし辺\(BF\)との交点を\(H\)とおく
\(PG\)を\(x\)とおくと\(GH=(4-x)\)
それぞれの三角形の面積を\(x\)を用いて表すと
\(\triangle DEG=\cancelto{\color{red}2}{4}\times x\times\displaystyle\frac{1}{\cancelto{\color{red}1}{2}}=2x\)
\(\begin{align}\triangle BFG&=3\times(4-x)\times\displaystyle\frac{1}{2}\\&=\displaystyle\frac{3(4-x)}{2}\end{align}\)
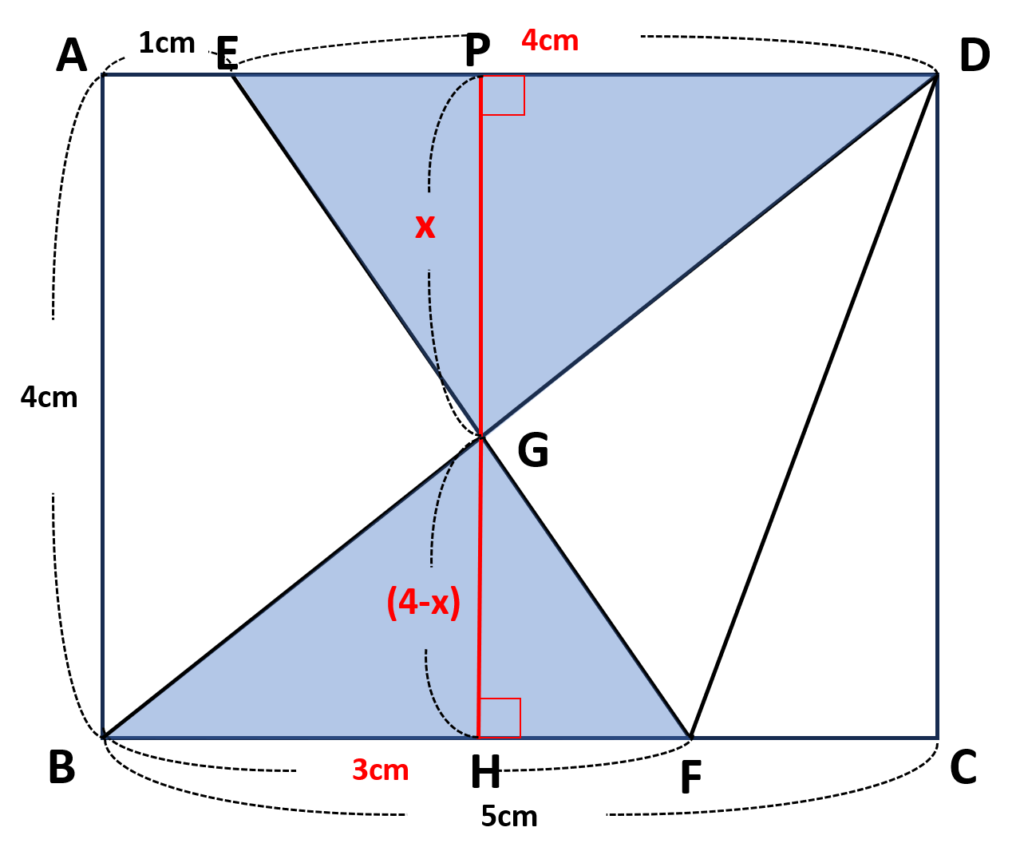

\(\triangle DEG:\triangle BFG=16:9\)より
\(2x:\displaystyle\frac{3(4-x)}{2}=16:9\)
\(\begin{align}2x\times9&=\displaystyle\frac{3(4-x)}{\cancelto{\color{red}1}{2}}\times\cancelto{\color{red}8}{16}\\\cancelto{\color{red}3}{18}x&=\cancelto{\color{red}4}{24}(4-x)\\3x&=4(4-x)\\3x&=16-4x\\3x+4x&=16\\7x&=16\\x&=\displaystyle\frac{16}{7}\end{align}\)


よって\(\triangle DEG\)の面積は
\(4\times\displaystyle\frac{\cancelto{\color{red}8}{16}}{7}\times\displaystyle\frac{1}{\cancelto{\color{red}1}{2}}=\displaystyle\frac{32}{7}\)
- 四角形\(ABCD=4\times5=20\)
- ①\(\triangle BCD=10\)
- ②\(\triangle DEG=\displaystyle\frac{32}{7}\)
よって、四角形\(ABGE\)の面積は
\(\begin{align}四角形ABGE&=20-10-\displaystyle\frac{32}{7}\\&=10-\displaystyle\frac{32}{7}\\&=\displaystyle\frac{70}{7}-\displaystyle\frac{32}{7}\\&=\displaystyle\frac{38}{7}\end{align}\)
解答. \(\displaystyle\frac{38}{7}cm^2\)
今回の解法以外にも複数の解き方があります
様々なパターンを増やしてどのような図形でも対応できるようにしておきましょう
(3)
\(\stackrel{\huge\frown}{DF}\)と弦\(DF\)で囲まれた面積を求める
・問題文からどのような定理や性質があるか
・導きたい面積をどう工夫すれば求められるか
を考えると必要な部分が見えてくる


- \(D, E, F\)が各辺の中点⇒中点連結定理の性質が利用できそう
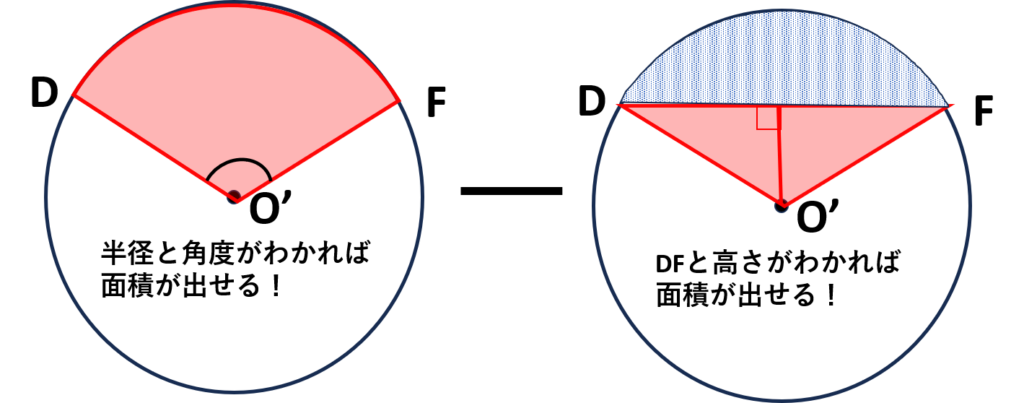
- 扇形\(O’DF-\triangle O’DF\)で答えは出せる
(小さい円の中心点を\(O’\)とする)
⇒小さい円の半径、角度、\(DF\)の長さ、\(\triangle O’DF\)の高さが必要
⇒中点連結定理と円周角、\(\angle{A}=60\text{°}\)を上手く組み合わせることがポイントになりそうと推測!
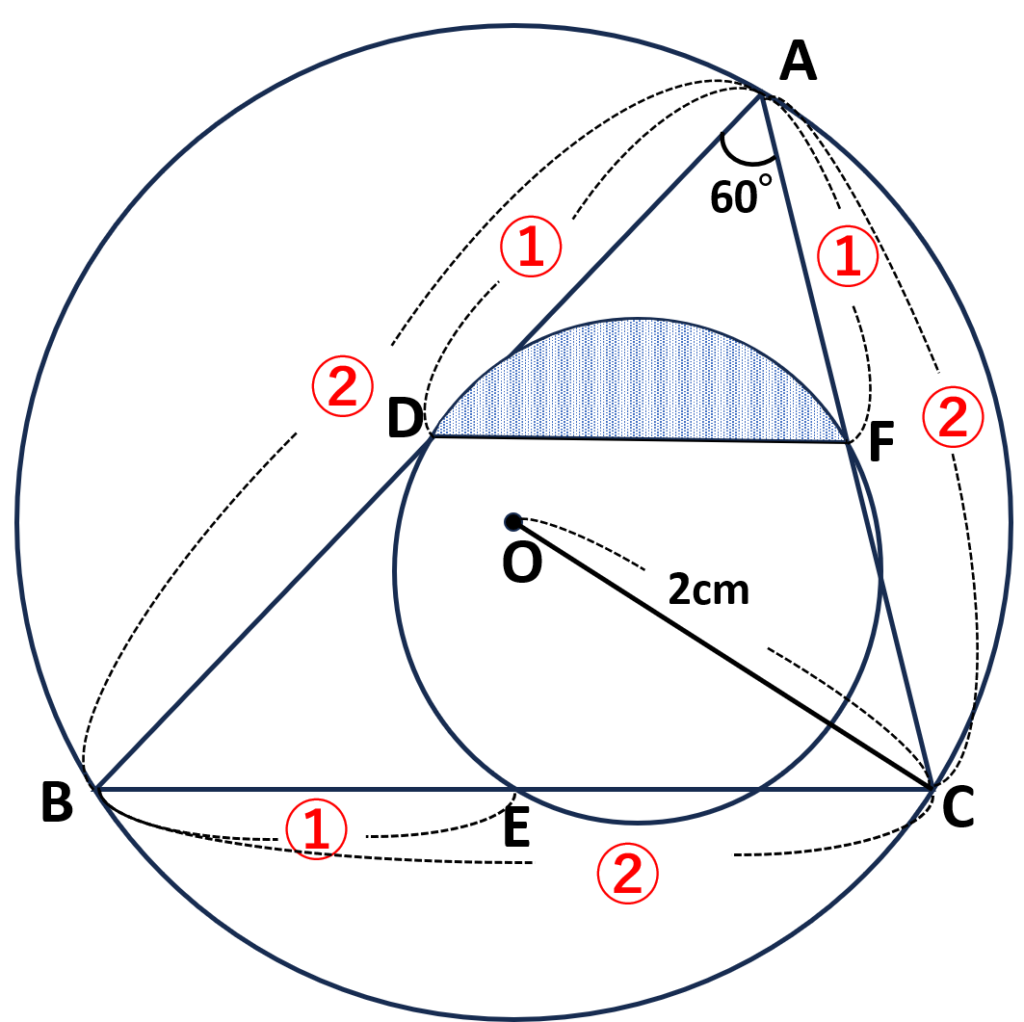


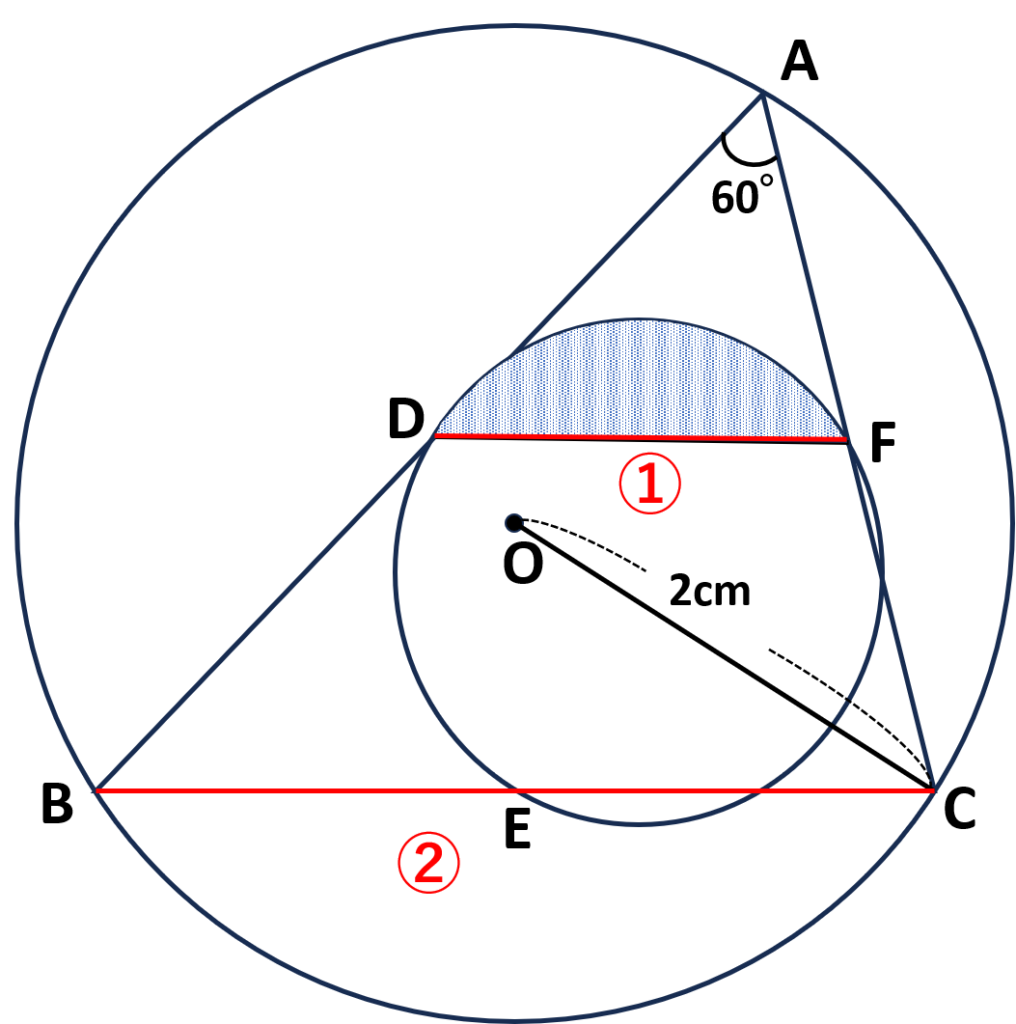
まずは既に描かれている\(DF\)の長さを求めたい
- 中点連結定理より\(DF=\displaystyle\frac{1}{2}BC\)
⇒\(BC\)の長さがわかれば\(DF\)は求められる

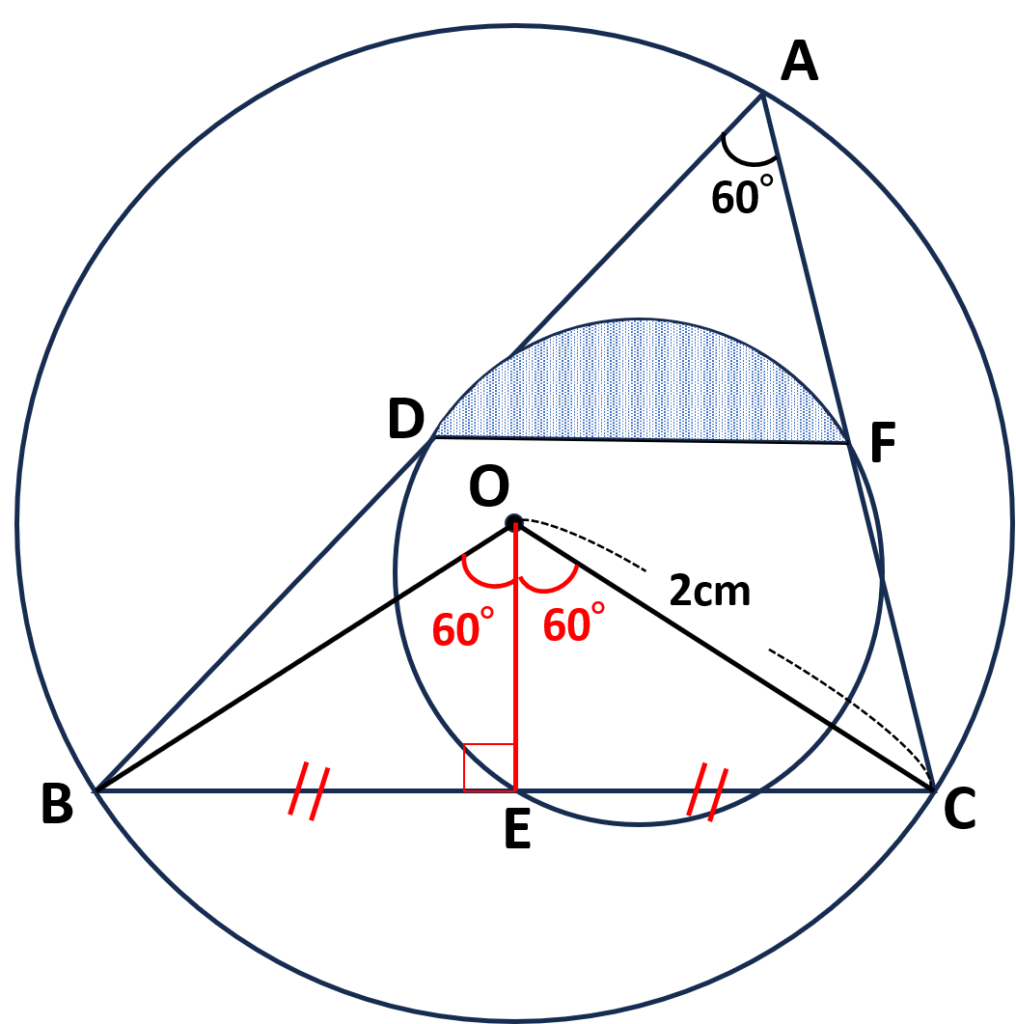
円周角と中心角の関係より
\(\begin{align}\angle{BOC}&=\angle{A}\times2\\&=60\text{°}\times2\\&=120\text{°}\end{align}\)


\(\triangle BOC\)は二等辺三角形より\(\angle{BOE}=60\text{°}\)
- \(OB,OC\)は円\(O\)の半径より\(OB=OC\)
- 頂角の二等分線は底辺を垂直に二等分する
\(\angle{BOE}=60\text{°}\)
\(\angle{OEB}=90\text{°}\)

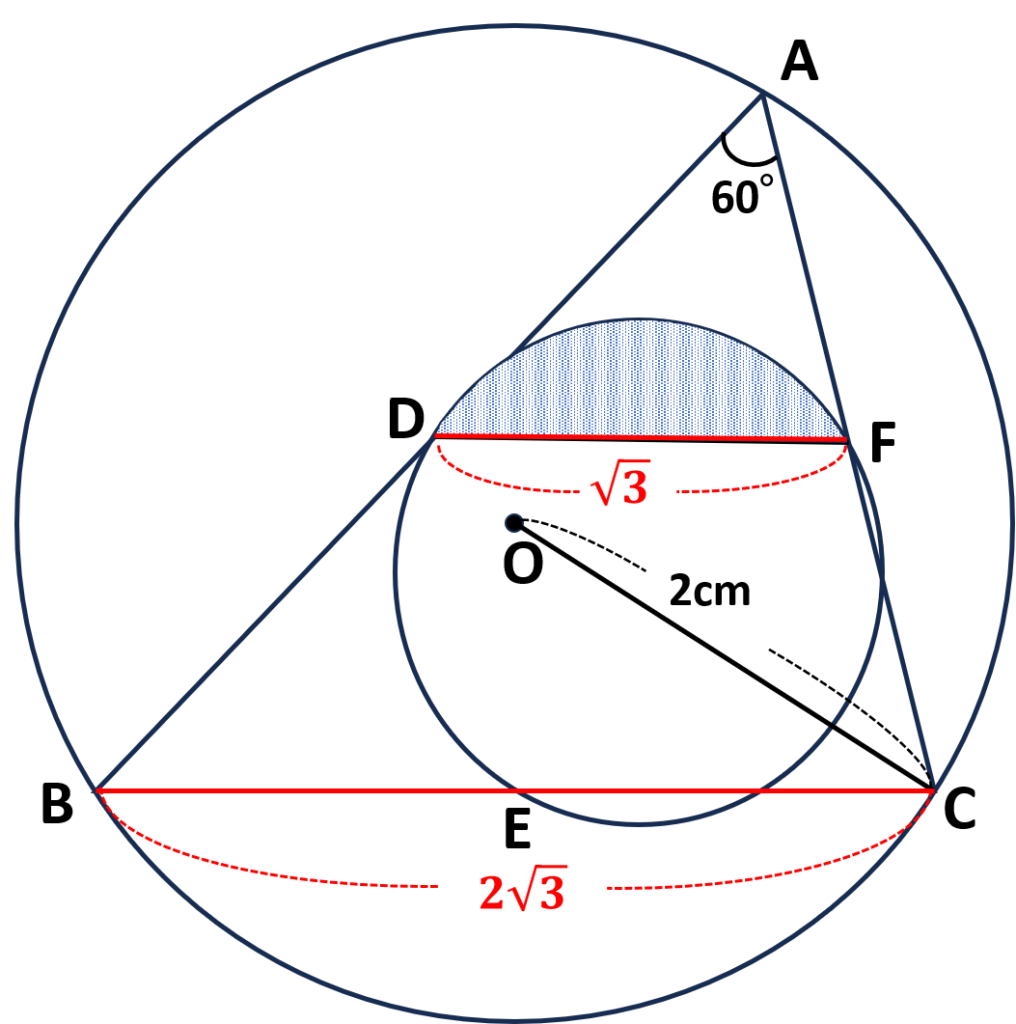
\(\triangle BOE\)は\(30\text{°},60\text{°},90\text{°}\)の直角三角形なので辺の比は
\(OE:BO:BE=1:2:\sqrt{3}\)
\(\begin{align}BO:BE&=2:\sqrt{3}\\2:BE&=2:\sqrt{3}\\\cancelto{\color{red}1}{2}BE&=\cancelto{\color{red}1}{2}\sqrt{3}\\BE&=\sqrt{3}\end{align}\)
\(BC=2BE=2\sqrt{3}\)より
\(DF=\displaystyle\frac{1}{2}BC=\displaystyle\frac{1}{\cancelto{\color{red}1}{2}}\times\cancelto{\color{red}1}{2}\sqrt{3}=\sqrt{3}\)



次に扇形\(O’DF\)の中心角を求めていきたい
- 小さい円に注目すると\(\angle{DEF}\)は\(\stackrel{\huge\frown}{DF}\)の円周角であることがわかる
⇒\(\angle{DEF}\)がわかれば、その中心角の\(\angle{DO’F}\)が出せる
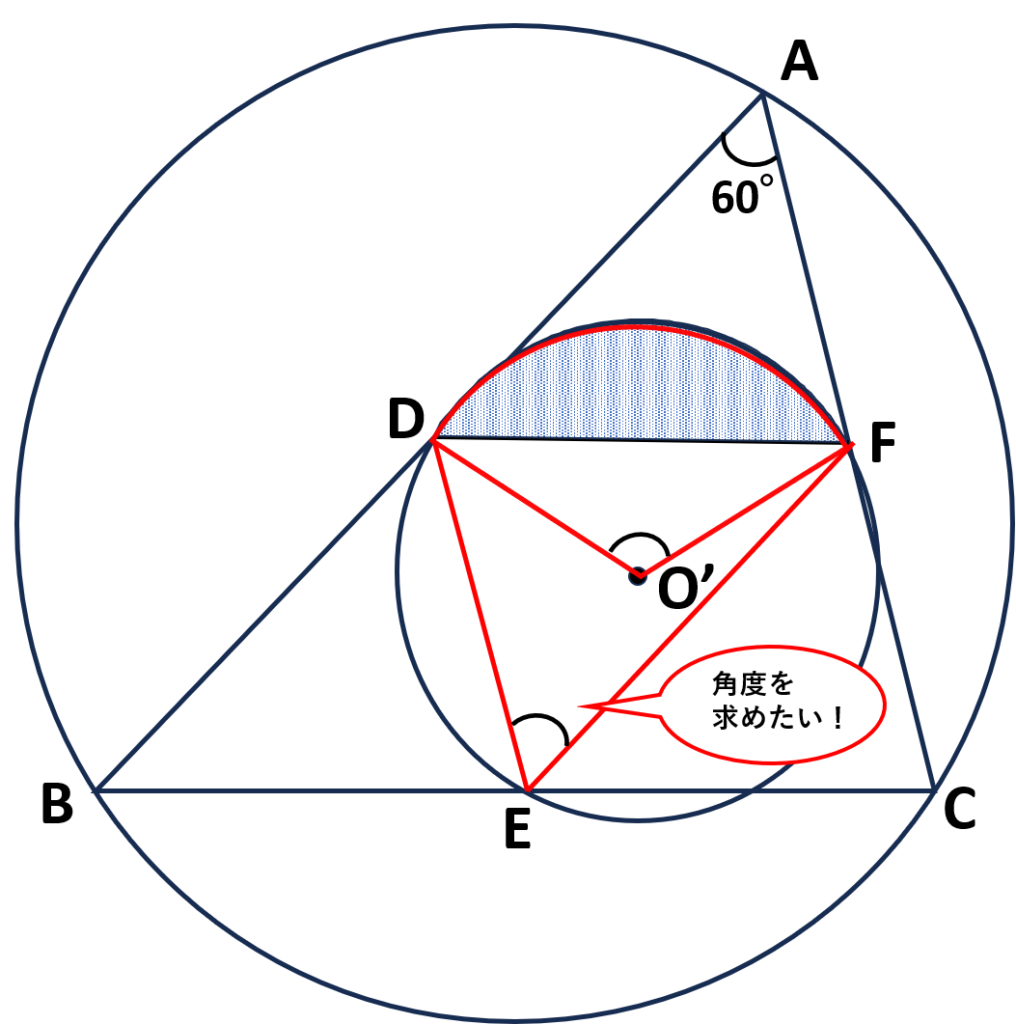

\(\angle{DEF}\)を求めるために、再度\(\triangle ABC\)の中点連結定理を利用する
- 中点連結定理より\(DE/\!/FA、EF/\!/DA\)がいえる
⇒四角形\(ABFE\)は平行四辺形なので対角が等しい
⇒\(\angle{DAF}=\angle{DEF}=60\text{°}\)
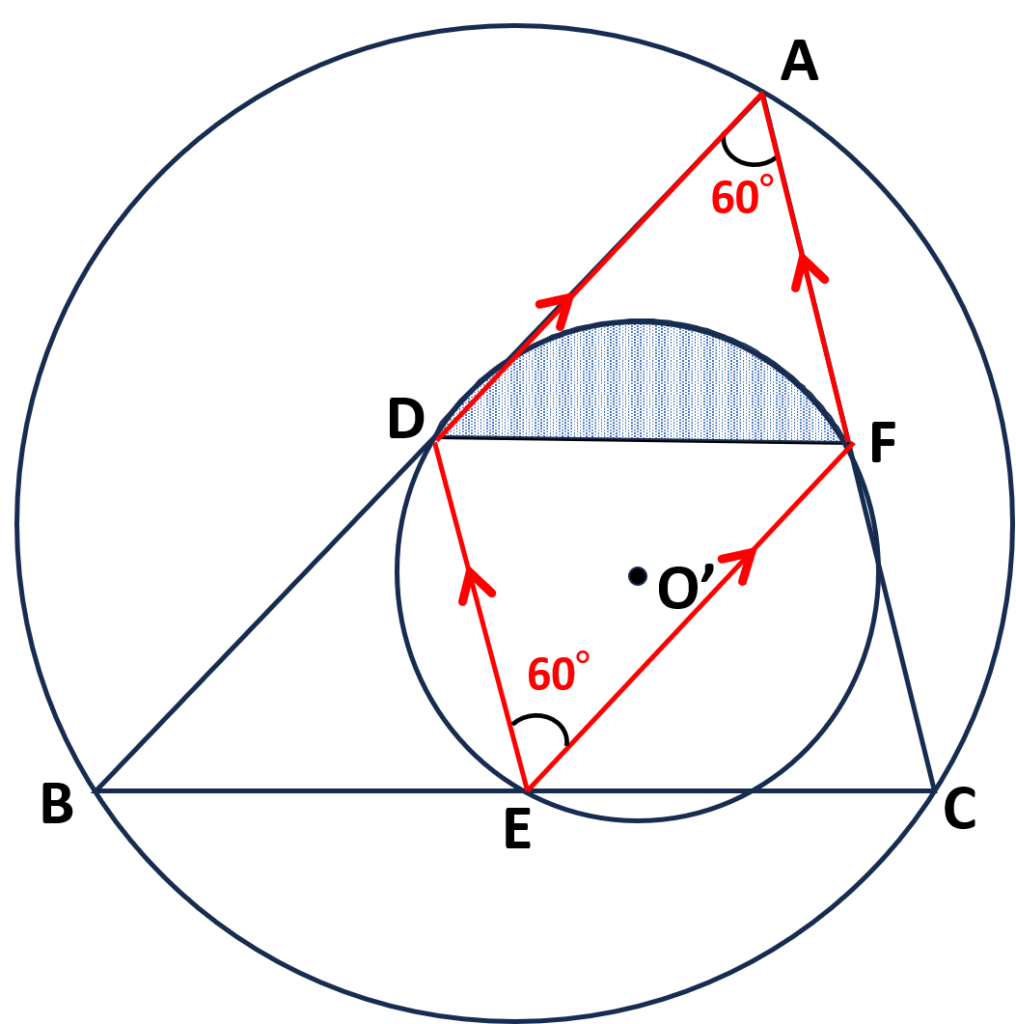

\(\triangle BDEと\triangle BAC\)において
・\(\angle{B}\)は共通
・点\(D\)は\(AB\)の中点より\(BD:BA=1:2\)
・点\(E\)は\(BC\)の中点より\(BE:BC=1:2\)
2組の辺の比とその間の角が等しいので
\(\therefore\triangle BDE\unicode[sans-serif]{x223D}\triangle BAC\)
相似な図形の対応する角は等しいので\(\angle{BDE}=\angle{BAC}\)
(\(\angle{BED}=\angle{BCA}\)でも良い)
同位角が等しいので\(DE/\!/CA(=FA)\)
\(\triangle CEFと\triangle CBA\)においても同様のことがいえるので
\(EF/\!/AB(=AD)\)
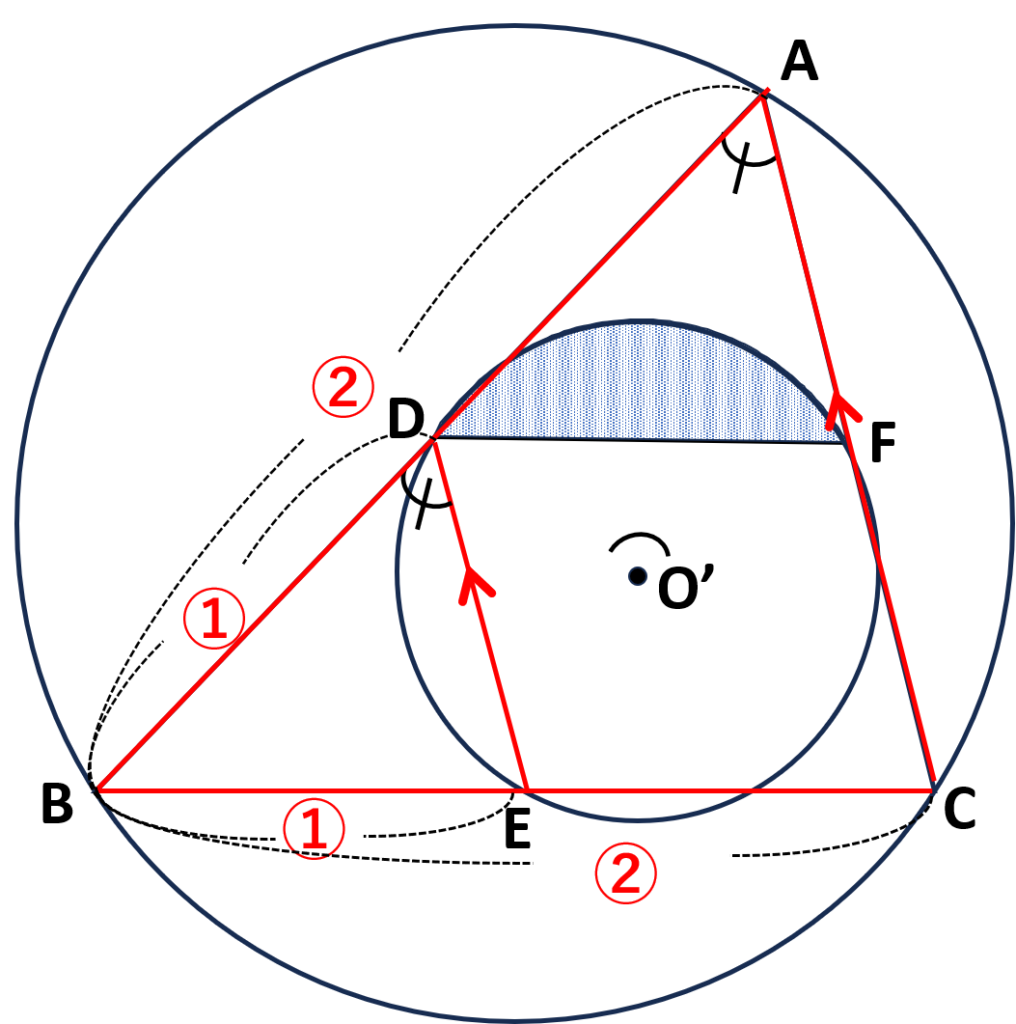

\(\triangle BDE\unicode[sans-serif]{x223D}\triangle BAC\)
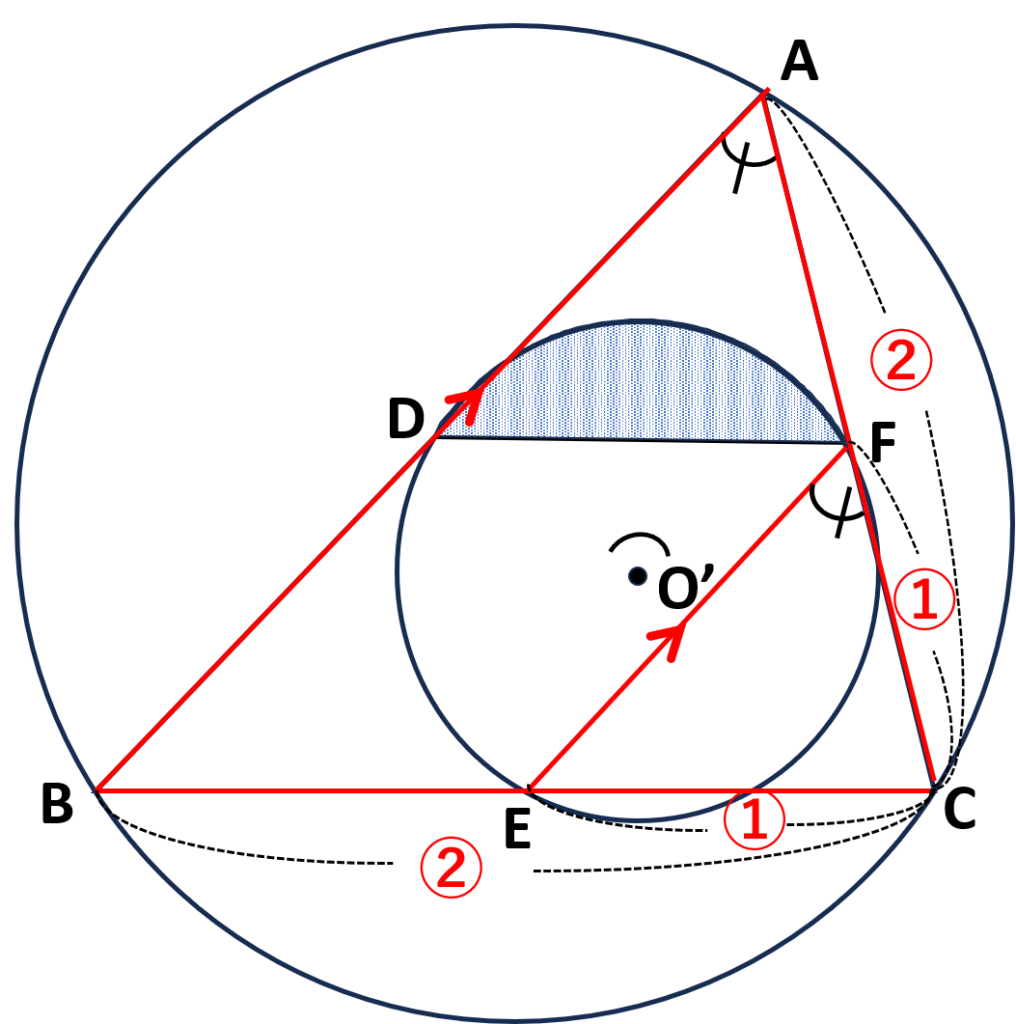

\(\triangle CEF\unicode[sans-serif]{x223D}\triangle CBA\)
\(\angle{DEF}=60\text{°}\)とわかったので円周角と中心角の関係より
\(\begin{align}\angle{DO’F}&=\angle{DEF}\times2\\&=60\text{°}\times2\\&=120\text{°}\end{align}\)
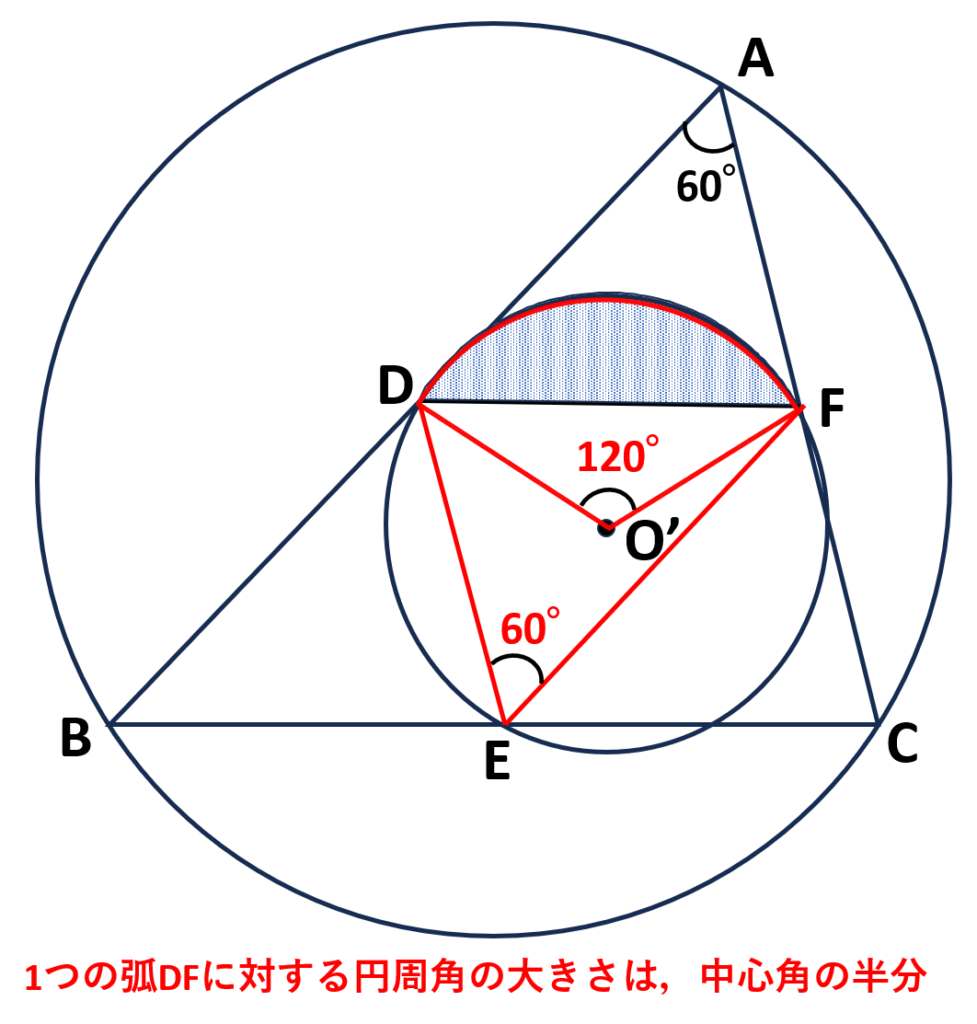

ここまでで\(DF\)の長さと扇形の角度がわかったので、あとは小さい円の半径と\(\triangle O’DF\)の高さを求めていく
- 扇形\(O’DF-\triangle O’DF\)
- 小さい円の半径⇒?
- 扇形の角度⇒\(120\text{°}\)
- \(DF\)の長さ⇒\(\sqrt{3}\)
- \(\triangle O’DF\)の高さ⇒?
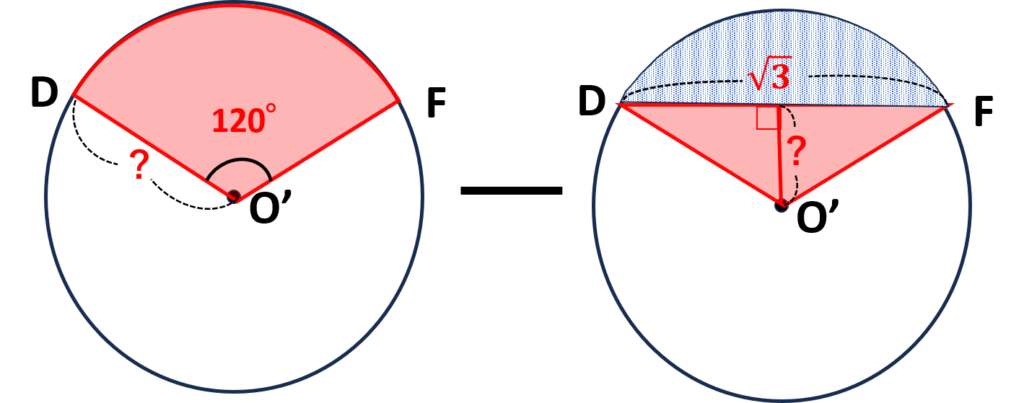

\(\triangle DO’F\)に注目すると、\(O’D,O’F\)はともに円\(O’\)の半径なので
\(O’D=O’F\)の二等辺三角形であることがわかる
点\(O’\)から\(DF\)に下ろした垂線と\(DF\)の交点を\(H\)とすると
\(\begin{align}\angle{DO’H}&=\angle{DO’F}\times\displaystyle\frac{1}{2}\\&=120\text{°}\times\displaystyle\frac{1}{2}=60\text{°}\end{align}\)
\(\begin{align}DH=HF&=\displaystyle\frac{1}{2}\times DF\\&=\displaystyle\frac{1}{2}\times\sqrt{3}\\&=\displaystyle\frac{\sqrt{3}}{2}\end{align}\)
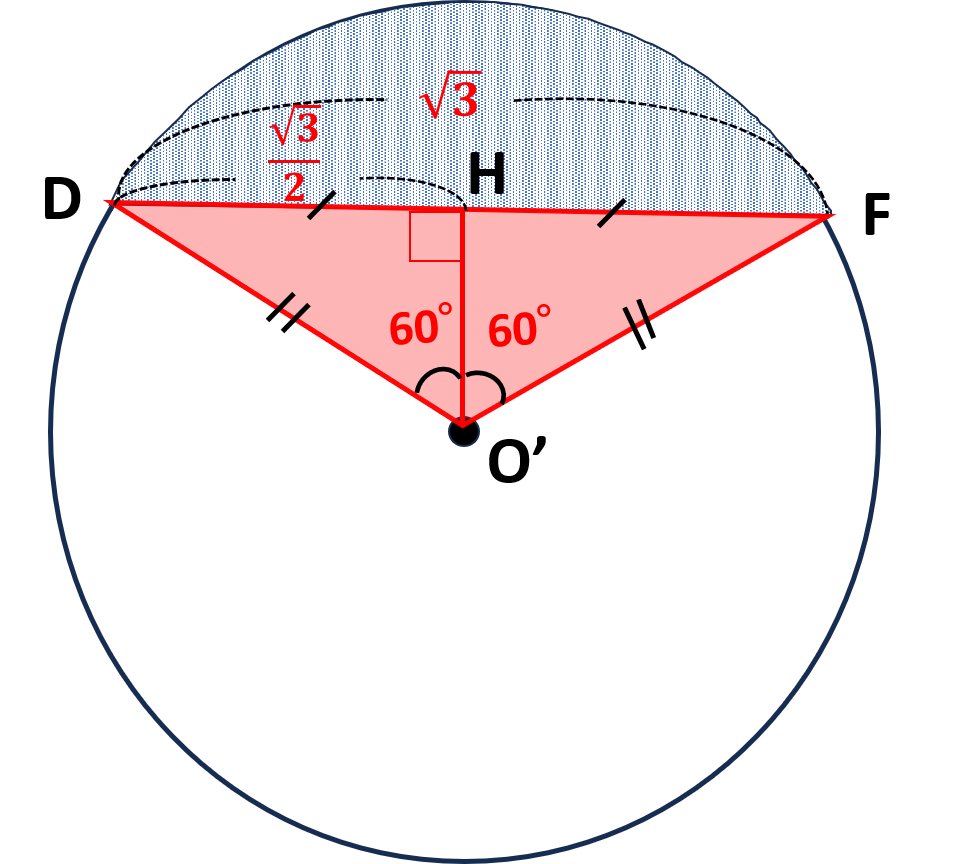

\(\triangle DO’H\)は\(30\text{°},60\text{°},90\text{°}\)の直角三角形なので辺の比は
\(O’H:O’D:DH=1:2:\sqrt{3}\)
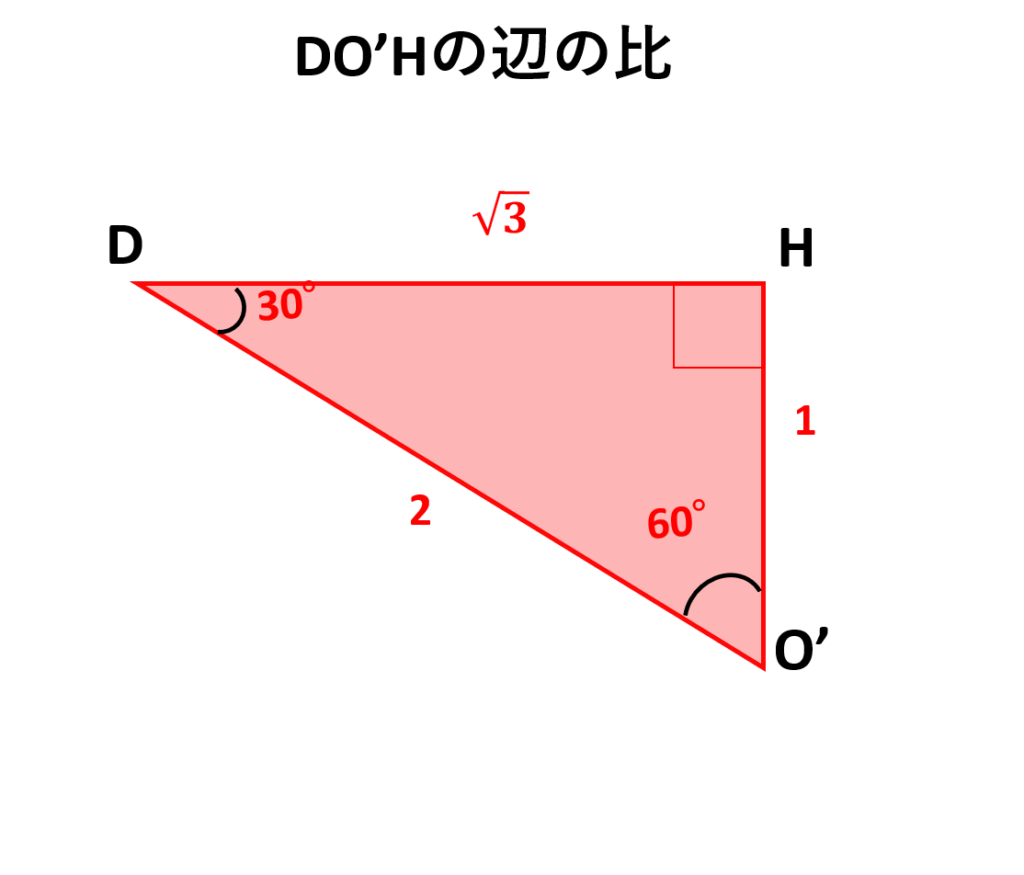

\(DH=\displaystyle\frac{\sqrt{3}}{2}\)なので
\(O’H\)の長さは
\(\begin{align}O’H:DH&=1:\sqrt{3}\\O’H:\displaystyle\frac{\sqrt{3}}{2}&=1:\sqrt{3}\\\cancelto{\color{red}1}{\sqrt{3}}\times O’H&=\displaystyle\frac{\cancelto{\color{red}1}{\sqrt{3}}}{2}\times1\\O’H&=\displaystyle\frac{1}{2}\end{align}\)
同様に\(O’D\)の長さは
\(\begin{align}O’H:O’D&=1:2\\\displaystyle\frac{1}{2}:O’D&=1:2\\1\times O’D&=\displaystyle\frac{1}{\cancelto{\color{red}1}{2}}\times\cancelto{\color{red}1}{2}\\O’D&=1\end{align}\)


これで必要な情報が全て揃ったので問題の面積を求めていく
- 扇形\(O’DF-\triangle O’DF\)
- 小さい円の半径⇒\(1\)
- 扇形の角度⇒\(120\text{°}\)
- \(DF\)の長さ⇒\(\sqrt{3}\)
- \(\triangle O’DF\)の高さ⇒\(\displaystyle\frac{1}{2}\)
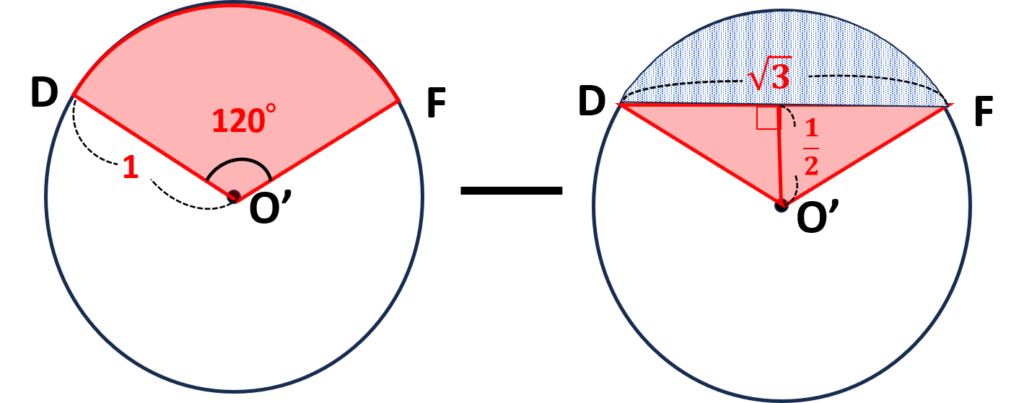

<扇形の面積の求め方>
\((半径)^2\times\pi\times\displaystyle\frac{中心角}{360}\)
\(\begin{align}扇形O’DF&=1^2\times\pi\times\displaystyle\frac{\cancelto{\color{red}1}{120}}{\cancelto{\color{red}3}{360}}\\&=\displaystyle\frac{\pi}{3}\end{align}\)
\(\begin{align}\triangle O’DF&=\sqrt{3}\times\displaystyle\frac{1}{2}\times\displaystyle\frac{1}{2}\\&=\displaystyle\frac{\sqrt{3}}{4}\end{align}\)
よって、求めたい面積は
扇形\(O’DF-\triangle O’DF=\displaystyle\frac{\pi}{3}-\displaystyle\frac{\sqrt{3}}{4}\)
解答. \(\displaystyle\frac{\pi}{3}-\displaystyle\frac{\sqrt{3}}{4}\)
問題文を読んだ時点でどのような定理が使えるかを予測できるようにするのが大切!
・それぞれ中点をとる⇒中点連結定理
・円と図形⇒中心角、円周角
すぐに解法が出てこない場合は時間をかけずに他の問題へ切り替えましょう!
問題3
(1)
\(2\)つのさいころ\(A,B\)を同時に投げて、\(2\)つの目の数の積が\(10\)の約数になる確率を求める
・\(10\)の約数は\(1,2,5,10の4\)個
・\(2\)つの数を掛けて\(1,2,5,10\)のいずれかになる場合を考える
・さいころの目は\(1~6\)
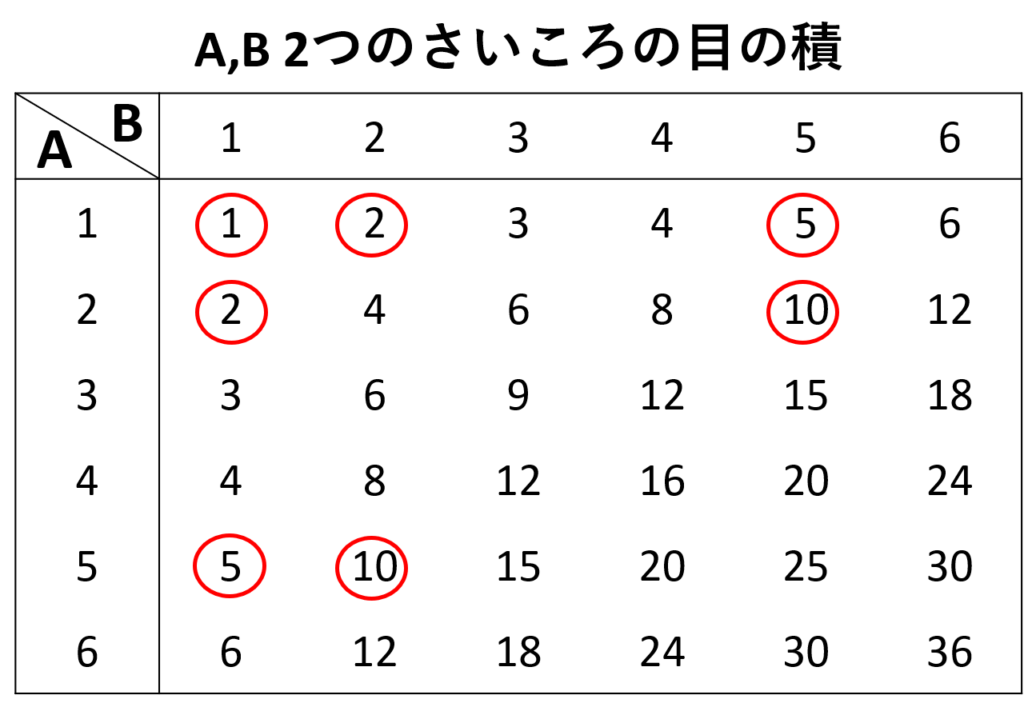
さいころ\(2\)つの目の積が\(1,2,5,10\)のいずれかになる場合は
\((1,1)\)\((1,2)\)\((1,5)\)\((2,1)\)\((2,5)\)\((5,1)\)\((5,2)\)の\(7\)通り
\(2\)つの目のさいころの組み合わせは全部で\(36\)通りなので
\(\displaystyle\frac{(それが起こる場合の数)}{(全体の場合の数)}=\displaystyle\frac{7}{36}\)
解答. \(\displaystyle\frac{7}{36}\)
漏れがないか不安な場合は
樹形図や表を用いて数えると良い



(2)
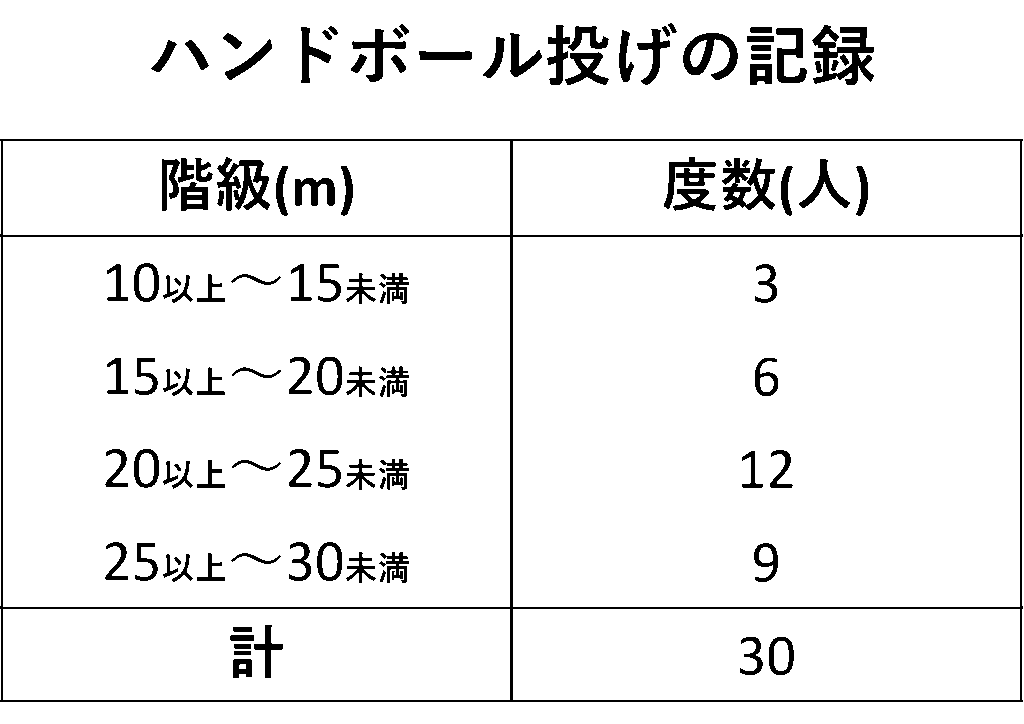
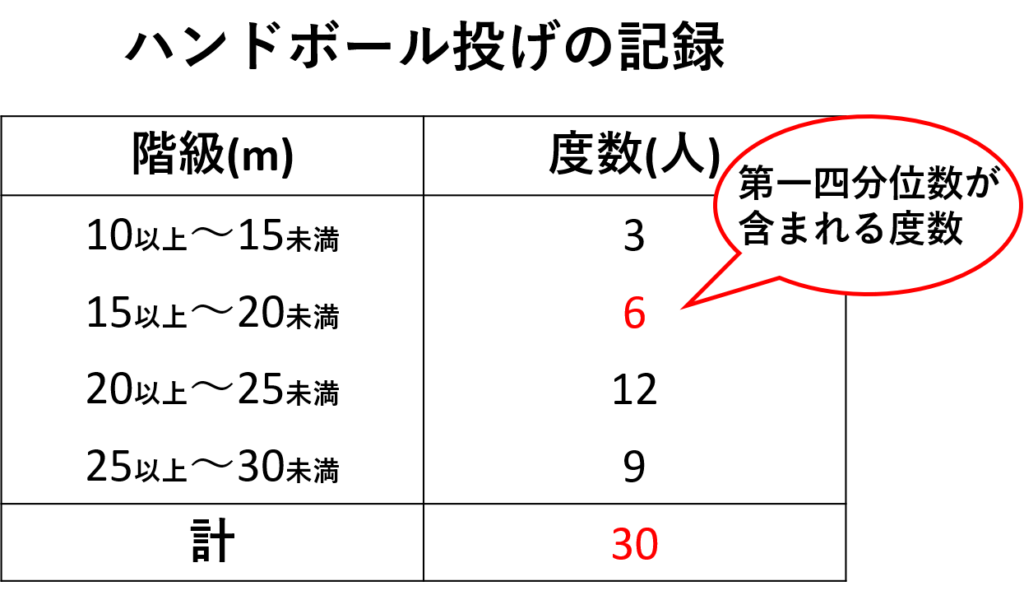
\(30\)人のハンドボール投げの記録の第一四分位数を含む階級の相対度数を求める
・四分位数とはデータを\(4\)分割する仕切り部分
・データの小さい順に第一、第二、第三となる
⇩⇩
・四分位数の問題はデータの分け方が大切
・データが偶数個か奇数個かで計算方法が異なるので注意!



しっかり分け方を理解できていれば四分位数の問題は難しくないよ!得点源にしていこう!

- \(30\)人を小さい順に並べる
- 第二四分位数を求める
- 第一四分位数を求める
- 第一四分位数の階級の相対度数を計算
まずは対象の\(30\)人を小さい順に並べていきます
横に並べても良いですが、今回は与えられた表があるのでそれを利用します
右の列に人数の累計を書き足していくと、どの階級までで累計何人いるかがわかります
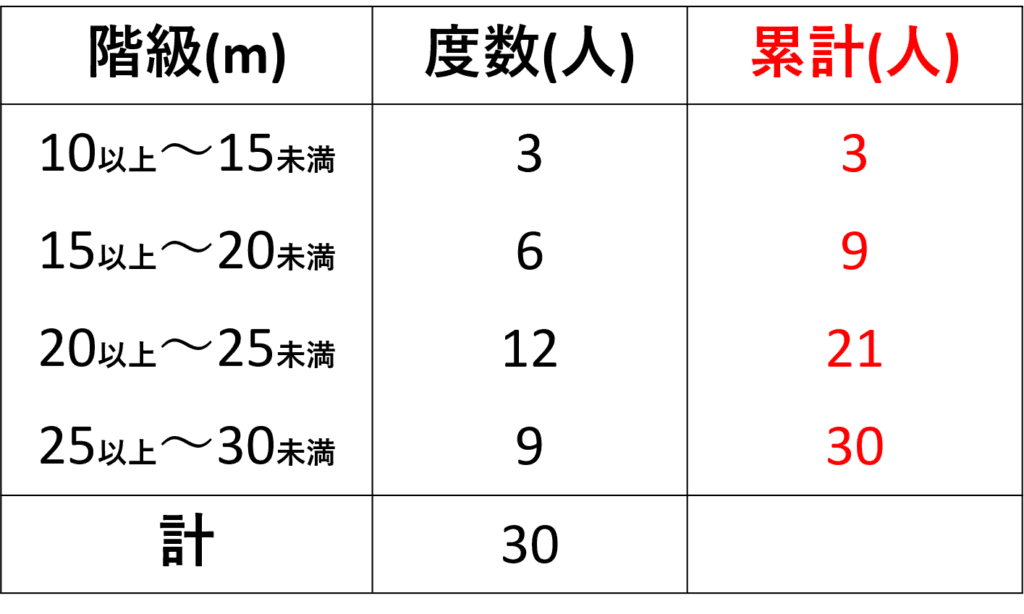

- \(30\)人を小さい順に並べる
- 第二四分位数を求める
⇒次ココ! - 第一四分位数を求める
- 第一四分位数の階級の相対度数を計算
<第二四分位数は?>
・データのちょうど半分の値
・データの数が偶数か奇数かで四分位数の求め方が異なるので注意!
《奇数の場合》
⇒ちょうど半分のところにあるデータの値を採用!
求め方
- (データの数)\(\div2\)をする
- 答え(商)に\(+1\)をしたデータの値を採用
(例:データの数が\(11\)個ある場合)
\(11\div2=5余り1\)
⇒\(5+1=6\)番目の値を採用する


《偶数の場合》
⇒ちょうど半分のところにある\(2\)つのデータの値を平均した値
・偶数の場合は綺麗に半分に割れる
⇒ちょうど真ん中のデータがない
⇒じゃあ中央の\(2\)つの平均にしよう!
という考え方です


求め方
- (データの数)\(\div2\)をする
- 答えと答えに\(+1\)をしたデータの値を平均して求める
(例:データの数が\(10\)個ある場合)
\(10\div2=5\)
⇒\(5\)番目と\(6\)番目の値の平均をとる
今回の場合は\(30\)人のデータ
⇒偶数パターンで計算
\(30\div2=15\)
⇒\(15\)番目と\(16\)番目の平均値が第二四分位数
今回のデータでいうと
階級\(20~25(m)\)の範囲に第二四分位数がいることがわかる


- \(30\)人を小さい順に並べる
- 第二四分位数を求める
- 第一四分位数を求める
⇒次ココ! - 第一四分位数の階級の相対度数を計算
第一四分位数は第二四分位数で分かれた小さいほうのデータを更に半分に分けた値です



考え方は第二四分位数と同じです
- 第二四分位数で分かれた小さいデータ\(15\)が対象
データの数が\(15\)⇒奇数なので
\(15\div2=7余り1\)より第一四分位数は\(7+1=8\)番目のデータ
今回のデータでは階級\(15~20(m)\)の範囲に第一四分位数(\(8\)番目のデータ)が入る




- \(30\)人を小さい順に並べる
- 第二四分位数を求める
- 第一四分位数を求める
- 第一四分位数の階級の相対度数を計算⇒最後ココ!
<相対度数とは?>
各カテゴリの度数を総度数で割った値
今回のデータでは階級\(15~20(m)\)の範囲に第一四分位数が入るので
・第一四分位数を含む階級の度数:\(6\)(人)
・総度数:\(30\)人(総人数)
よって第一四分位数の相対度数は
\(6\div30=0.2\)
解答. \(0.2\)

(3)
ア \(y=-\displaystyle\frac{1}{2}x^2\)において、\(x\)の値が\(1\)から\(3\)まで増加するときの変化の割合を求める
\(変化の割合=\displaystyle\frac{(yの増加量)}{(xの増加量)}\)
<\(x\)の増加量>
\((変化後のx値)-(変化前のx値)\)
<\(y\)の増加量>
\((変化後のy値)-(変化前のy値)\)
\((xの増加量)=3-1=2\)
\(\begin{align}(yの増加量)&=-\displaystyle\frac{1}{2}(3)^2-(-\displaystyle\frac{1}{2}(1)^2)\\&=-\displaystyle\frac{9}{2}-(-\displaystyle\frac{1}{2})\\&=-\displaystyle\frac{9}{2}+\displaystyle\frac{1}{2}\\&=-\displaystyle\frac{\cancelto{\color{red}4}{8}}{\cancelto{\color{red}1}{2}}=-4\end{align}\)
よって変化の割合は
\(\begin{align}変化の割合&=\displaystyle\frac{(yの増加量)}{(xの増加量)}\\&=\displaystyle\frac{-\cancelto{\color{red}2}{4}}{\cancelto{\color{red}1}{2}}\\&=-2\end{align}\)
解答. \(-2\)
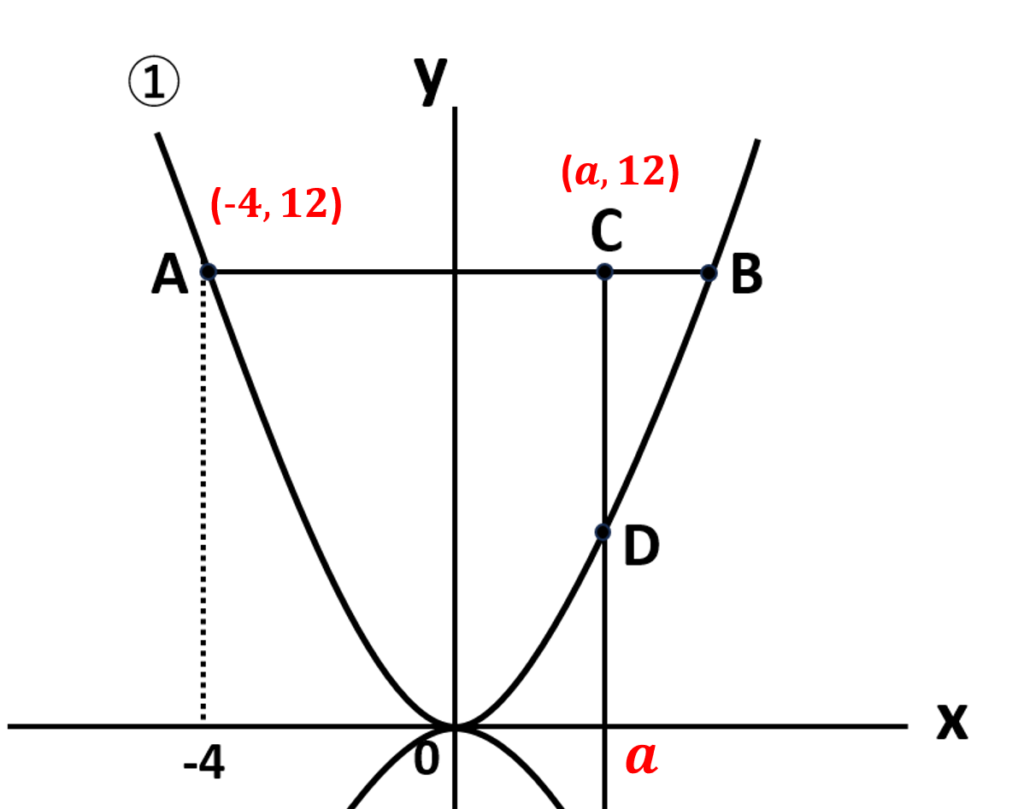
イ 線分\(CD=DE\)のときの点\(C\)の\(x\)座標を求める(\(x\)座標を\(a\)として\(a\)の値を求める)
・\(①y=\displaystyle\frac{3}{4}x^2、②y=-\displaystyle\frac{1}{2}x^2\)
・線分\(AB\)は\(x\)軸に平行
・点\(C\)は線分\(AB\)上の点で\(x\)座標は正の数(点\(B\)と異なる点)
・点\(C\)を通り\(y\)軸に平行な直線をひき、放物線①、②との交点をそれぞれ\(D,E\)とする


- 点\(C,点D,点Eのy\)座標を\(a\)を使って表す
- \(CD,DE\)の長さを\(a\)を使って表す
- \(CD=DE\)の方程式を解いて\(a\)を出す
①点\(D\)、点\(E\)はそれぞれ放物線①、放物線②上なので
点\(D=(a,\displaystyle\frac{3}{4}a^2)\)
点\(E=(a,-\displaystyle\frac{1}{2}a^2)\)


点\(C\)の\(y\)座標は点\(A\)の\(y\)座標と等しい
点\(A\)の\(y\)座標は\(y=\displaystyle\frac{3}{4}x^2\)の\(x=-4\)のときの値なので
\(\begin{align}点Aのy座標&=\displaystyle\frac{3}{4}\times(-4)^2\\&=\displaystyle\frac{3}{\cancelto{\color{red}1}{4}}\times\cancelto{\color{red}4}{16}=12\end{align}\)
よって
点\(C=(a,12)\)

- 点\(C,点D,点Eのy\)座標を\(a\)を使って表す⇒OK!
点\(C=(a,12)\)
点\(D=(a,\displaystyle\frac{3}{4}a^2)\)
点\(E=(a,-\displaystyle\frac{1}{2}a^2)\) - \(CD,DE\)の長さを\(a\)を使って表す
- \(CD=DE\)の方程式を解いて\(a\)を出す


次に②\(CD,DE\)の長さを\(a\)を使って表していく
- 点\(C,点D,点Eのy\)座標を\(a\)を使って表す⇒OK!
- \(CD,DE\)の長さを\(a\)を使って表す⇒次ココ!
- \(CD=DE\)の方程式を解いて\(a\)を出す
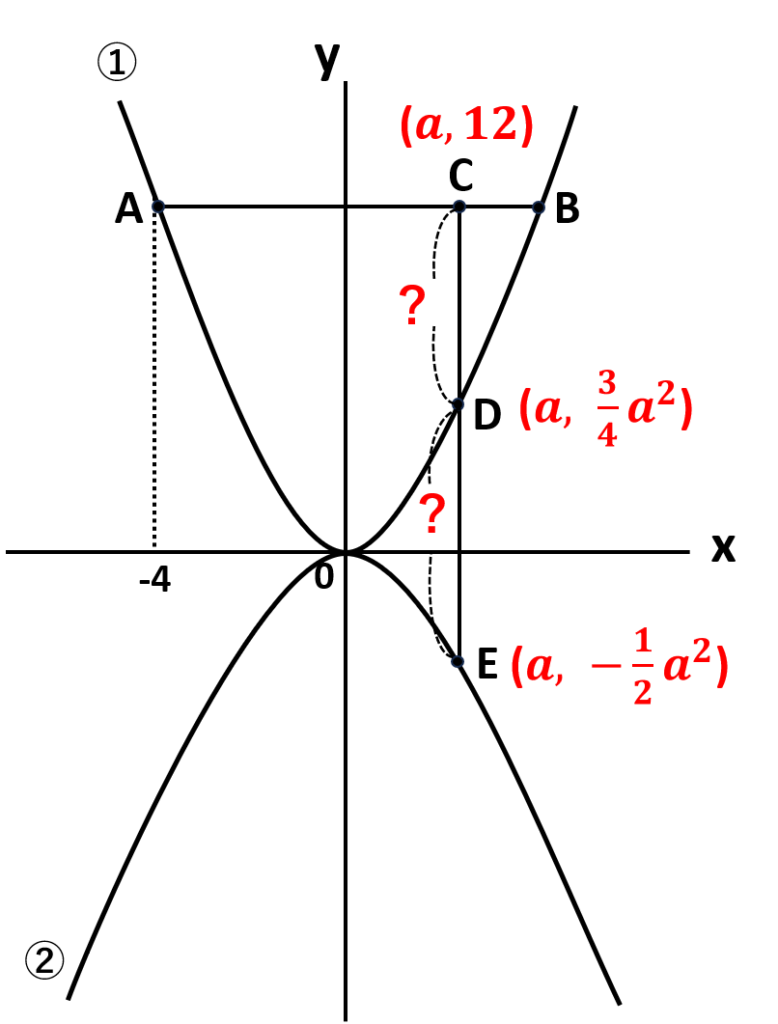
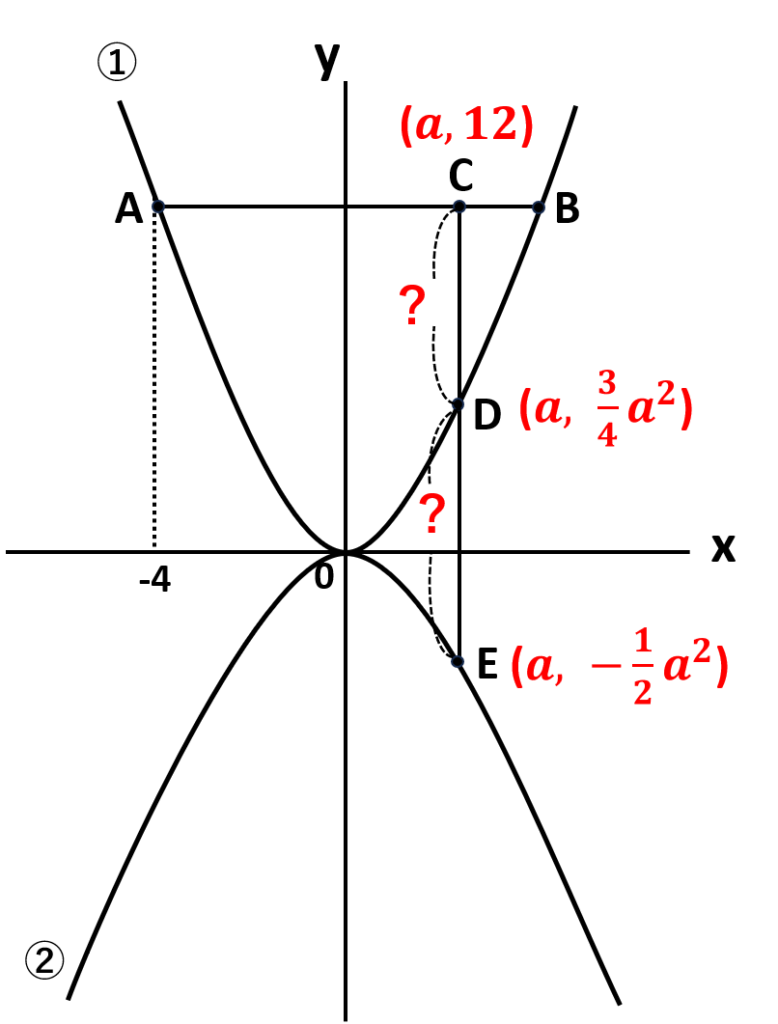
\(C,D,E\)は全て\(y\)軸に平行なので、\(y\)座標同士の差で計算すれば\(CD,DE\)の長さは求められる



長さを求めるときは\(y\)座標の大きいものから小さいものを引くようにしましょう!
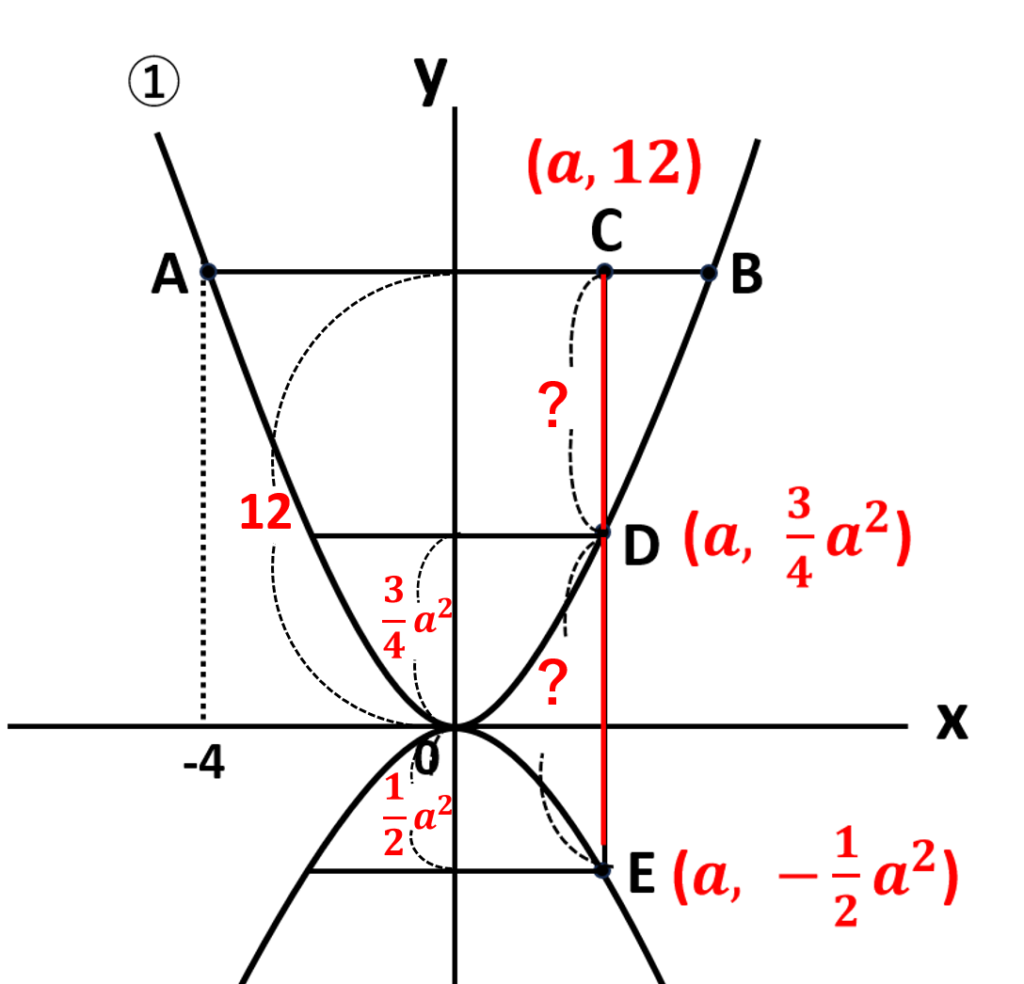
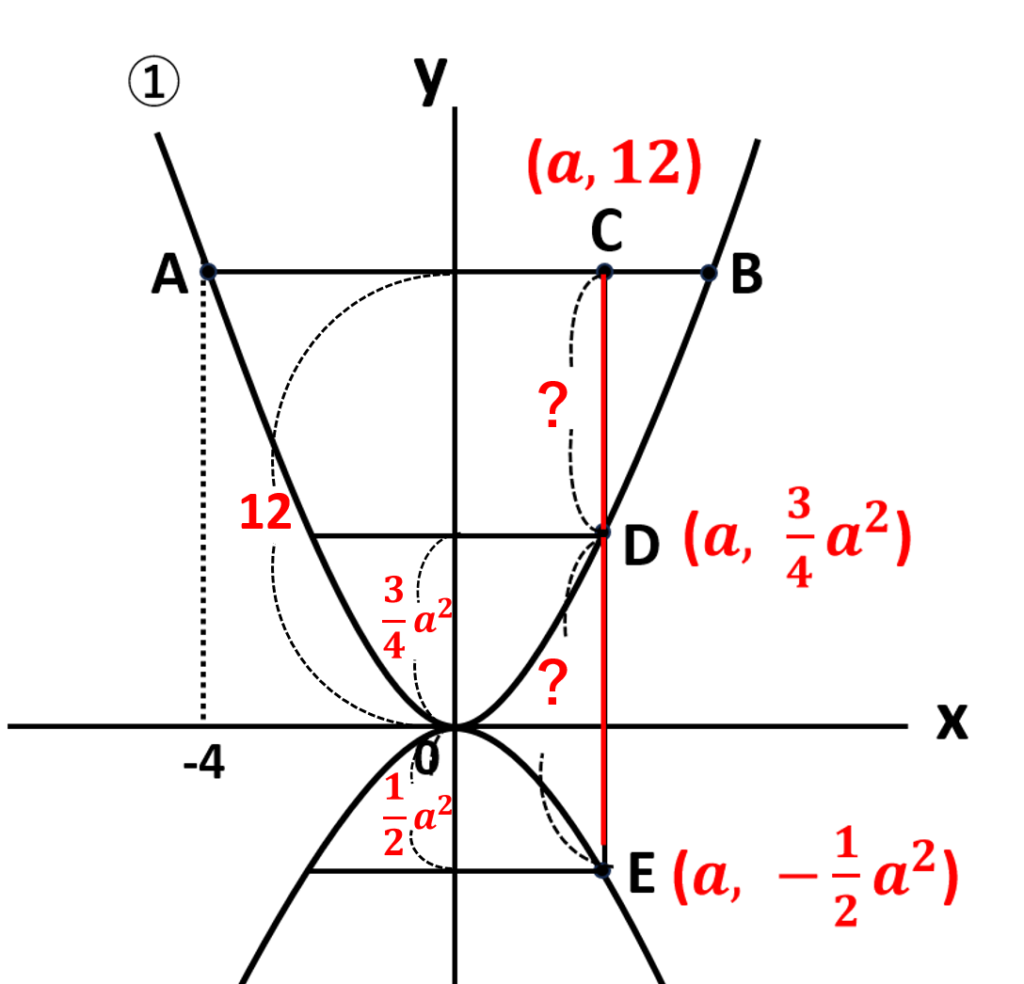
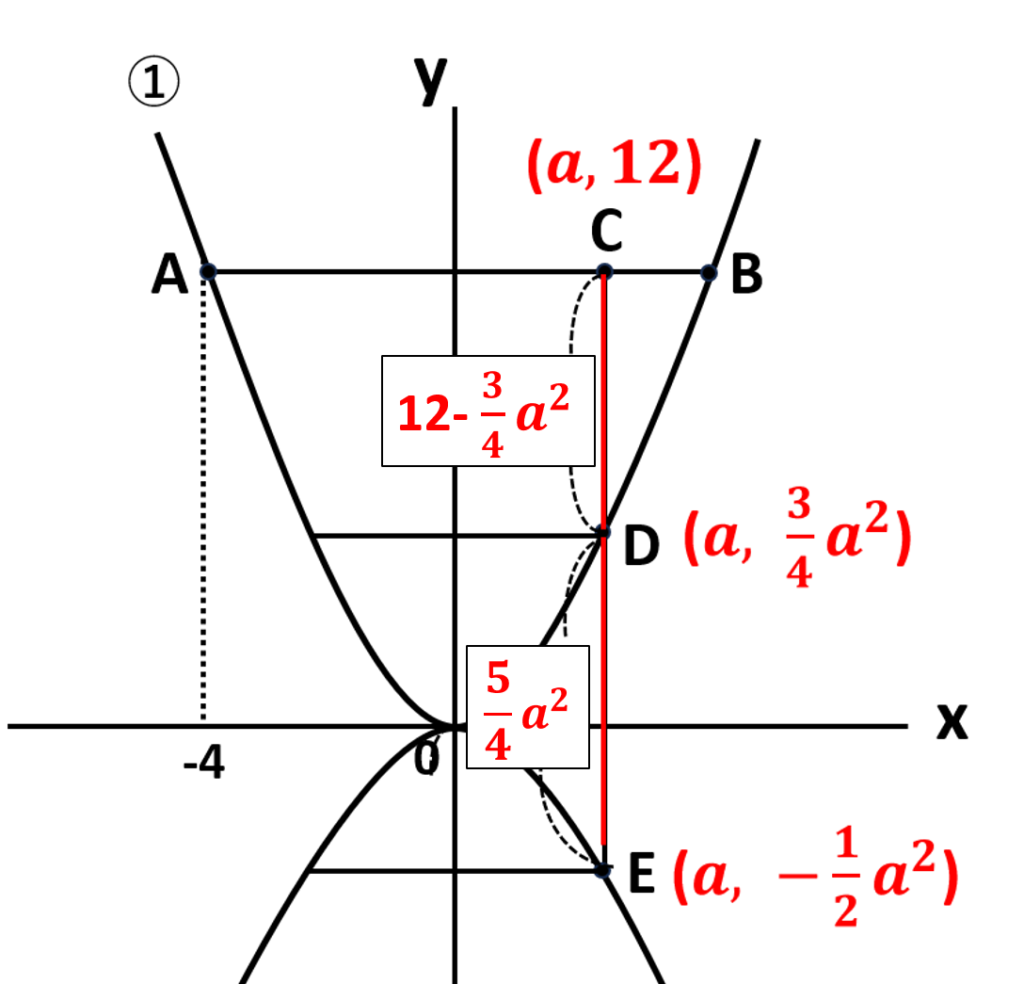
\(\begin{align}CD&=(Cのy座標)-(Dのy座標)\\&=12-\displaystyle\frac{3}{4}a^2\end{align}\)
\(\begin{align}DE&=(Dのy座標)-(Eのy座標)\\&=\displaystyle\frac{3}{4}a^2-(-\displaystyle\frac{1}{2}a^2)\\&=\displaystyle\frac{3}{4}a^2+\displaystyle\frac{1}{2}a^2\\&=\displaystyle\frac{3}{4}a^2+\displaystyle\frac{2}{4}a^2\\&=\displaystyle\frac{5}{4}a^2\end{align}\)

- 点\(C,点D,点Eのy\)座標を\(a\)を使って表す⇒OK!
- \(CD,DE\)の長さを\(a\)を使って表す⇒OK!
- \(CD=DE\)の方程式を解いて\(a\)を出す
\(CD,DE\)の長さが出たので、
\(CD=DE\)となるときの\(a\)の値を求める
\(CD=12-\displaystyle\frac{3}{4}a^2\)
\(DE=\displaystyle\frac{5}{4}a^2\)より
\(12-\displaystyle\frac{3}{4}a^2=\displaystyle\frac{5}{4}a^2\)
全体に\(-1\)をかけて計算しやすくすると
\(\begin{align}\displaystyle\frac{3}{4}a^2-12&=-\displaystyle\frac{5}{4}a^2\\\displaystyle\frac{3}{4}a^2+\displaystyle\frac{5}{4}a^2&=12\\\displaystyle\frac{\cancelto{\color{red}2}{8}}{\cancelto{\color{red}1}{4}}a^2&=12\\\cancelto{\color{red}1}{2}a^2&=\cancelto{\color{red}6}{12}\\a^2&=6\end{align}\)
\(a\)は正の数なので、\(a=\sqrt{6}\)
解答. \(a=\sqrt{6}\)
(4)
\(2\)つの奇数をそれぞれ\(2\)乗してできた\(2\)つの数の和に\(2\)を加えた数は\(4\)の倍数であることを文字式を使って証明する



証明問題は自分の中で「完成形」をイメージしてから逆算で解いていこう!
\(4\)の倍数であることを文字式を使って証明する
- 最後に持っていきたい形
⇒\(4\times(整数)\)の形にしたい
- \(2\)つの奇数を文字式を使って表す
- 問題文通りに計算をしていく
- 計算結果が\(4\times(整数)\)の形にする
まずは①\(2\)つの奇数を文字式を使って表す
文字式を使って奇数を表す方法
※\(m\)は整数とする
・\(2m+1\)または\(2m-1\)
どちらでもOK!
今回は\(2\)つの奇数なので、それぞれ別の文字式を使って表す必要がある
今回は\(2\)つの奇数を
- \(2m+1\)
- \(2n+1\)
とおく(\(m,n\)は整数)
- \(2\)つの奇数を文字式を使って表す
- 問題文通りに計算をしていく⇒次ココ
- 計算結果が\(4\times(整数)\)の形にする
問題文に書かれたとおりに\(2\)つの奇数を用いて「\(2\)つの奇数を\(2\)乗してできた\(2\)つの数の和に\(2\)を加える」を計算していく
\(\begin{align}&(2m+1)^2+(2n+1)^2+2\\&=\small{4m^2+4m+1+4n^2+4n+1+2}\\&=4m^2+4m+4n^2+4n+4\end{align}\)
- \(2\)つの奇数を文字式を使って表す
- 問題文通りに計算をしていく
- 計算結果が\(4\times(整数)\)の形にする⇒次ココ
先ほどの計算結果を\(4\times(整数)\)の形にしたいので\(4\)でくくると
\(\begin{align}&4m^2+4m+4n^2+4n+4\\&=4(m^2+m+n^2+n+1)\end{align}\)
\(m,n\)は整数より\((m^2+m+n^2+n+1)\)は整数
\(\therefore4(m^2+m+n^2+n+1)\)は\(4\)の倍数
問題4
(1)
<碁石の並べ方の問題>
・白と黒の碁石を並べる
・上段には白、黒を交互に並べる
・下段には黒、黒、白の順に繰り返し並べる





このように規則性のある問題は規則を一般化できるようにするのが大切だよ!
ア 上段下段\(2024\)列目まで碁石を置いたとき、\(2024\)列目の上段下段それぞれの碁石の色は?
- 上段は白、黒を交互に並べる
⇒偶数列は必ず黒の碁石になる - 下段は黒、黒、白の順で繰り返し
⇒\(3\)の倍数のみ白、それ以外は黒
\(2024\)は偶数なので
⇒上段は黒
\(2024\div3=674.666…\)より\(3\)で割り切れないので\(3\)の倍数ではない
⇒下段は黒
解答. 上段⇒㋑黒、下段⇒㋓黒
<\(3\)の倍数の見分け方>
・各桁の和が\(3\)の倍数かどうかで判断できる
\(2024\)の場合、\(2+0+2+4=8\)
\(8\)は\(3\)の倍数ではないので\(2024\)は\(3\)の倍数ではない
\(2025\)の場合、\(2+0+2+5=9\)
\(9\)は\(3\)の倍数なので\(2025\)は\(3\)の倍数



これを使うと時間短縮になるよ!
イ \(n\)列目まで碁石を置いたとき上段も下段も白の碁石であった。並んでいるすべての碁石のうち白の碁石の個数と黒の碁石の個数が比が\(8:11\)のときの\(n\)の値を求める
- 上段下段が白の碁石の場合のときを考える
- 上段下段の白、黒の個数を\(n\)を使って表す
- ②で表した個数と比を用いて\(n\)を求める
《上段下段が白の碁石になるときは?》
- 上段は白、黒を繰り返す
⇒奇数列(\(1,3,5\cdots\))のときに白になる - 下段は黒、黒、白を繰り返す
⇒\(3\)の倍数列(\(3,6,9\cdots\))のときに白になる
上段下段どちらも白の碁石になるためには奇数かつ\(3\)の倍数のときとわかる
- 上段下段が白の碁石の場合のときを考える
- 上段下段の白、黒の個数を\(n\)を使って表す⇒次ココ
- ②で表した個数と比を用いて\(n\)を求める
次に上段下段の白、黒の個数を\(n\)を使って表す
上段は白、黒の順番に並んでいる
⇒\(2\)列で[白、黒]の\(1\)セットが完成し、それを繰り返していく
⇒\(n\)が偶数の場合は\(\displaystyle\frac{n}{2}\)個で表せる



今回の場合は奇数列なので工夫が必要!


今回は奇数なのでそのまま半分にしてしまうと整数にならない
例)\(n=9\)の場合
\(9\div2=4.5\)となり碁石の個数として不適切
(碁石の個数は必ず整数)
奇数列の場合も偶数列と同じように[白、黒]の\(1\)セットの状態で半分にわれば整数の形が出てくるので、そのようにしてあげたい
例)\(n=9\)の場合
白、黒、白、黒、白、黒、白、黒、白の並び方なので
白が\(5\)個、黒が\(4\)個


白は\(10\)の半分(\(5\)個)、黒は\(8\)の半分(\(4\)個)なので
白:\(\displaystyle\frac{9+1}{2}\)、黒:\(\displaystyle\frac{9-1}{2}\)
で表すことができる
※白の個数=(黒の個数)\(+1\)で表しても良い



どちらも同じ値になるよ!


よって\(n\)列目のときの上段の白、黒の個数は
白:\(\displaystyle\frac{n+1}{2}\)、黒:\(\displaystyle\frac{n-1}{2}\)
と表すことができる





次は下段の碁石の個数を\(n\)で表そう!
下段は黒、黒、白の順番に並んでいる
⇒\(3\)列で[黒、黒、白]の\(1\)セットが完成し、それを繰り返していく
⇒今回\(n\)は\(3\)の倍数なのでちょうど[黒、黒、白]の\(1\)セットが完成した状態で終わっているはず


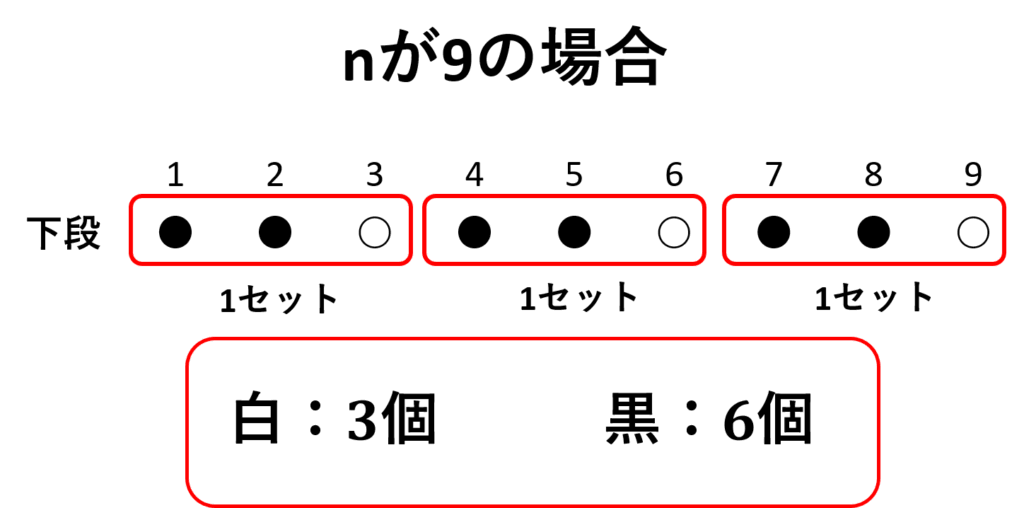
例)\(n=9\)の場合
黒、黒、白、黒、黒、白、黒、黒、白の並び方なので
白が\(3\)個、黒が\(6\)個

白は\(3\)回に\(1\)回出てくるので、
\(n=9\)の場合は\(9\times\displaystyle\frac{1}{3}=3\)
黒は\(3\)回に\(2\)回出てくるので、
\(n=9\)の場合は\(9\times\displaystyle\frac{2}{3}=6\)

今回は\(n\)が\(3\)の倍数なのでどちらも必ず整数になり碁石の個数として適切に表せる
\(3\)の倍数列のとき下段の白と黒の比率は常に
\(白:黒=1:2\)になる
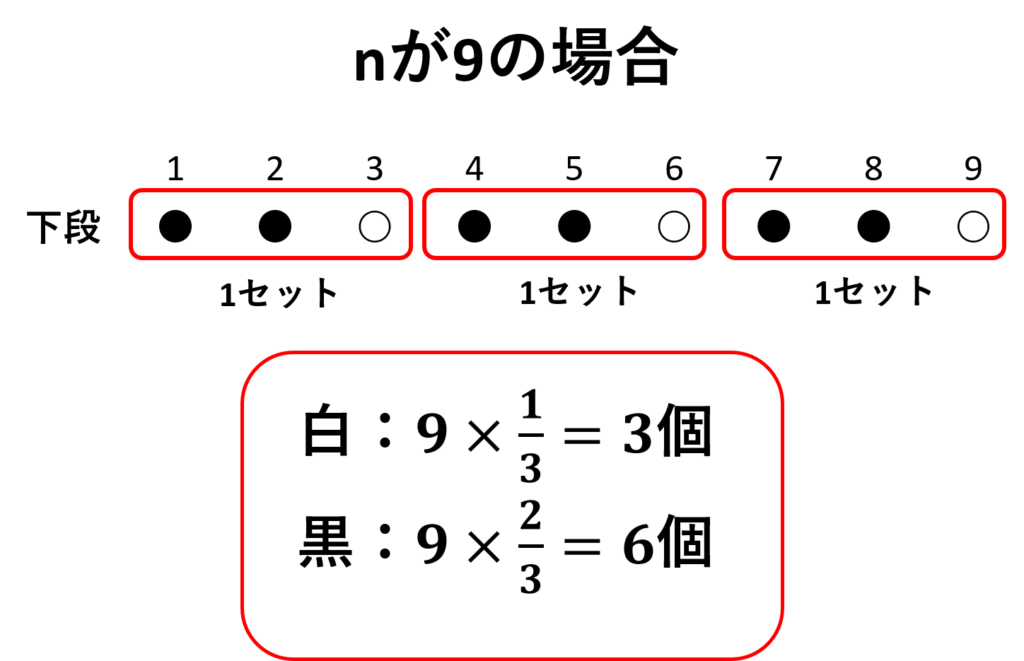
よって\(n=9\)の場合は
白:\(9\times\displaystyle\frac{1}{3}=3\)
黒:\(9\times\displaystyle\frac{2}{3}=6\)
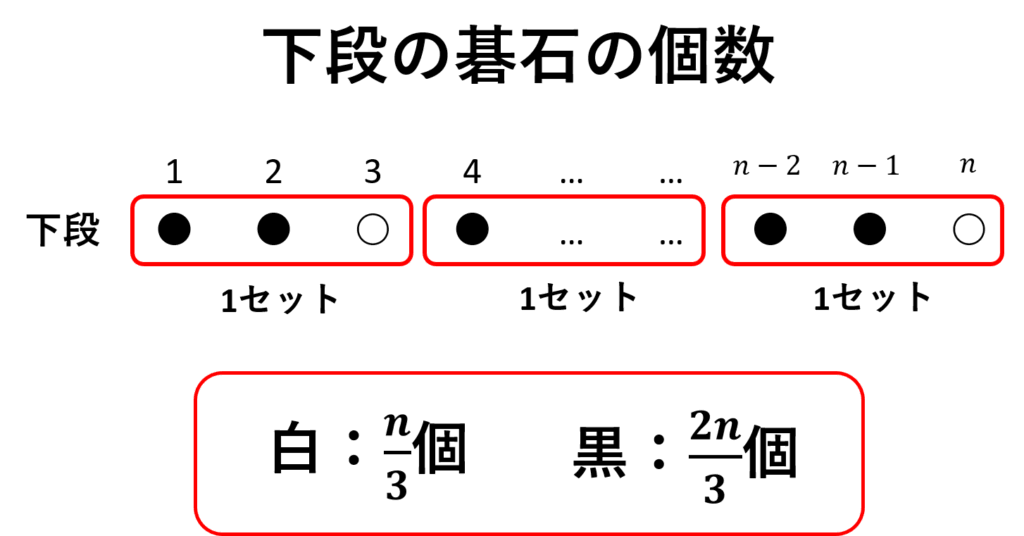
よって\(n\)列目のときの下段の白、黒の個数は
白:\(\displaystyle\frac{n}{3}\)個、黒:\(\displaystyle\frac{2n}{3}\)個
と表すことができる

- 上段下段が白の碁石の場合のときを考える
- 上段下段の白、黒の個数を\(n\)を使って表す
- ②で表した個数と比を用いて\(n\)を求める⇒次ココ
②より上段、下段の白、黒の個数を\(n\)を用いて表すと以下のようになる
上段の白、黒の個数
白:\(\displaystyle\frac{n+1}{2}\)、黒:\(\displaystyle\frac{n-1}{2}\)
下段の白、黒の個数
白:\(\displaystyle\frac{n}{3}\)個、黒:\(\displaystyle\frac{2n}{3}\)個



上段、下段を合わせた白、黒の碁石の数を求めよう!
上段、下段を合わせた白の個数
\(\begin{align}白の個数&=\displaystyle\frac{n+1}{2}+\displaystyle\frac{n}{3}\\&=\displaystyle\frac{3n+3}{6}+\displaystyle\frac{2n}{6}\\&=\displaystyle\frac{5n+3}{6}\end{align}\)
上段、下段を合わせた黒の個数
\(\begin{align}黒の個数&=\displaystyle\frac{n-1}{2}+\displaystyle\frac{2n}{3}\\&=\displaystyle\frac{3n-3}{6}+\displaystyle\frac{4n}{6}\\&=\displaystyle\frac{7n-3}{6}\end{align}\)
上段、下段を合わせた白の碁石の個数と黒の碁石の個数の比は\(8:11\)のときの\(n\)を求めたいので
\(\begin{align}(白の個数):(黒の個数)&=8:11\\\displaystyle\frac{5n+3}{6}:\displaystyle\frac{7n-3}{6}&=8:11\end{align}\)
\(8\times\displaystyle\frac{7n-3}{\cancelto{\color{red}1}{6}}=11\times\displaystyle\frac{5n+3}{\cancelto{\color{red}1}{6}}\)
↑両辺に\(6\)をかけて分母を払う
\(\begin{align}8\times(7n-3)&=11\times(5n+3)\\56n-24&=55n+33\\56n-55n&=33+24\\n&=57\end{align}\)
解答. \(n=57\)
(2)
<立体図形上を動く点の問題>
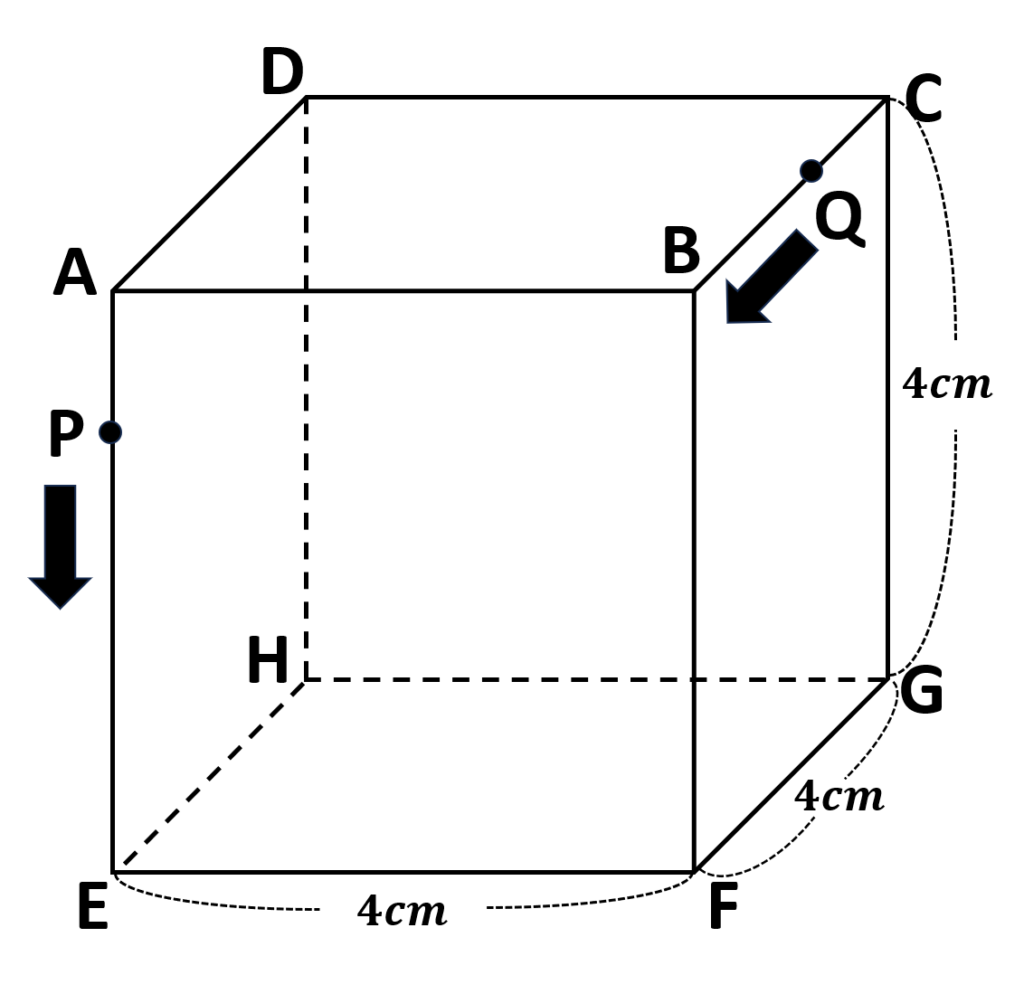
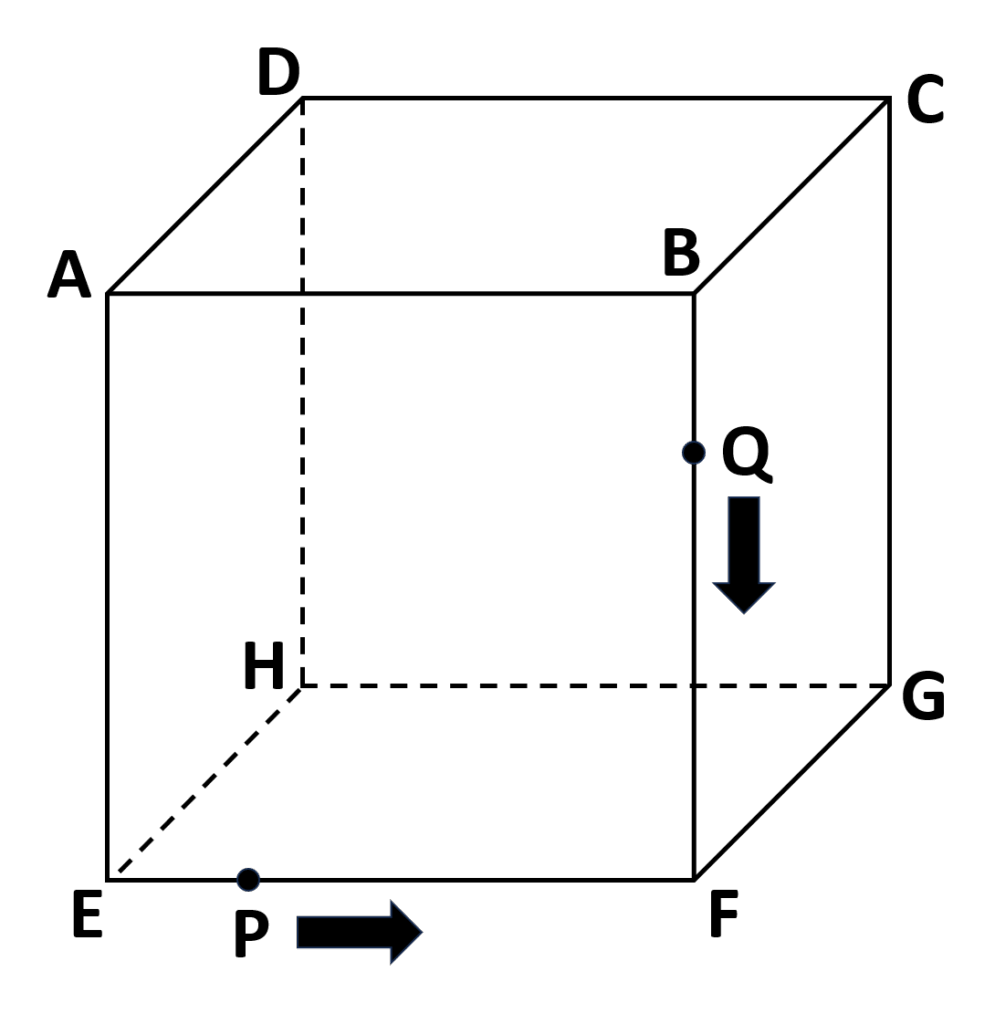
- \(1\)辺\(4cm\)の立方体
- 点\(P\)は点\(A\)を出発して辺\(AE,EF\)上を毎秒\(1cm\)の速さで点\(F\)まで動く
- 点\(Q\)は点\(C\)を出発して辺\(CB,BF\)上を毎秒\(1cm\)の速さで点\(F\)まで動く
- 点\(P,Q\)は同時に出発する


ア \(2\)点\(P,Q\)が同時に出発してから\(4\)秒後にできる三角すい\(APDQ\)の体積は何\(cm^3\)か。
- \(P,Q\)が\(4\)秒後にいる場所を確認し、三角すい\(APDQ\)の形を書く
- 底面、高さが求めやすい形を見つけ計算
まずは\(P,Q\)が\(4\)秒後にいる場所を図形に書き、どのような三角すいになるか確認しましょう
点\(P\)は点\(A\)を出発して毎秒\(1cm\)で点\(E\)に移動する
⇒\(AE=4cm\)なので\(4\)秒後、点\(P\)は点\(E\)にちょうど重なる
点\(Q\)は点\(C\)を出発して毎秒\(1cm\)で点\(B\)に移動する
⇒\(BC=4cm\)なので\(4\)秒後、点\(Q\)は点\(B\)にちょうど重なる
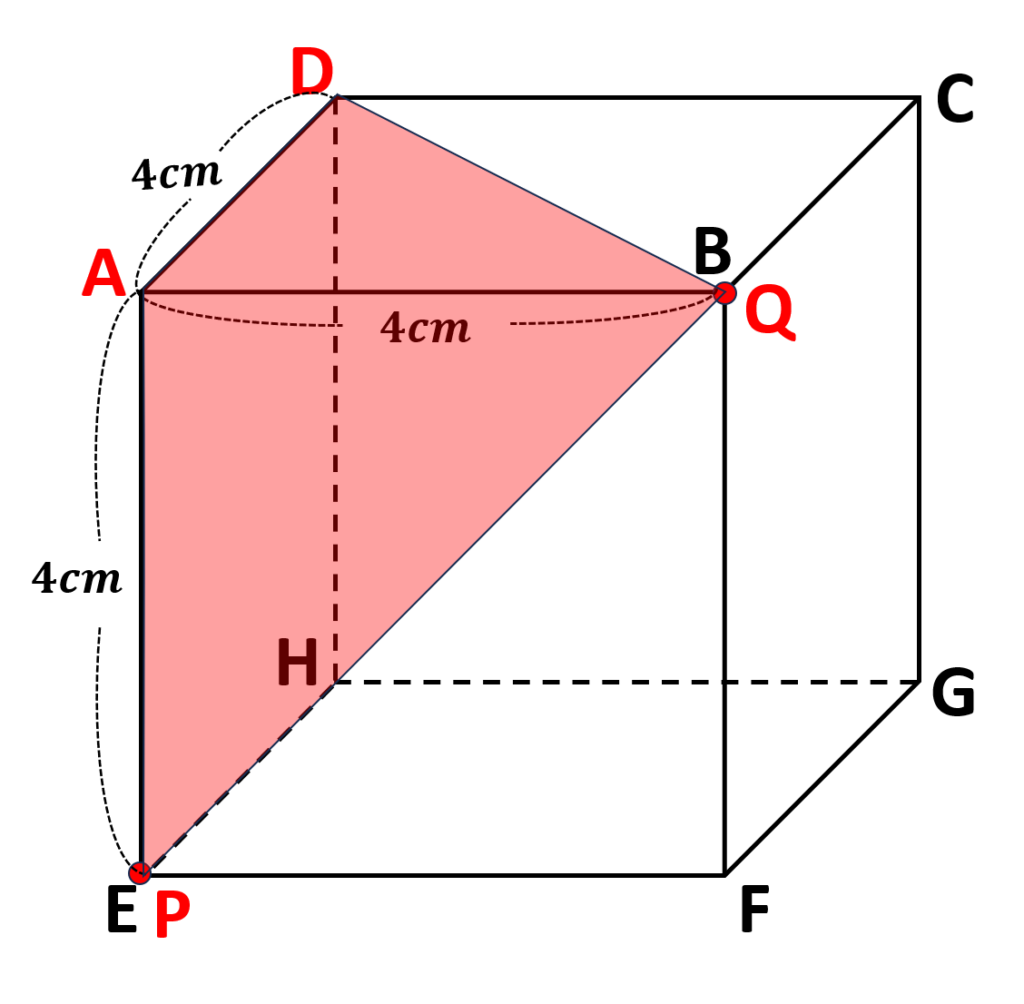

- \(P,Q\)が\(4\)秒後にいる場所を確認し、三角すい\(APDQ\)の形を書く
- 底面、高さが求めやすい形を見つけ計算⇒次ココ
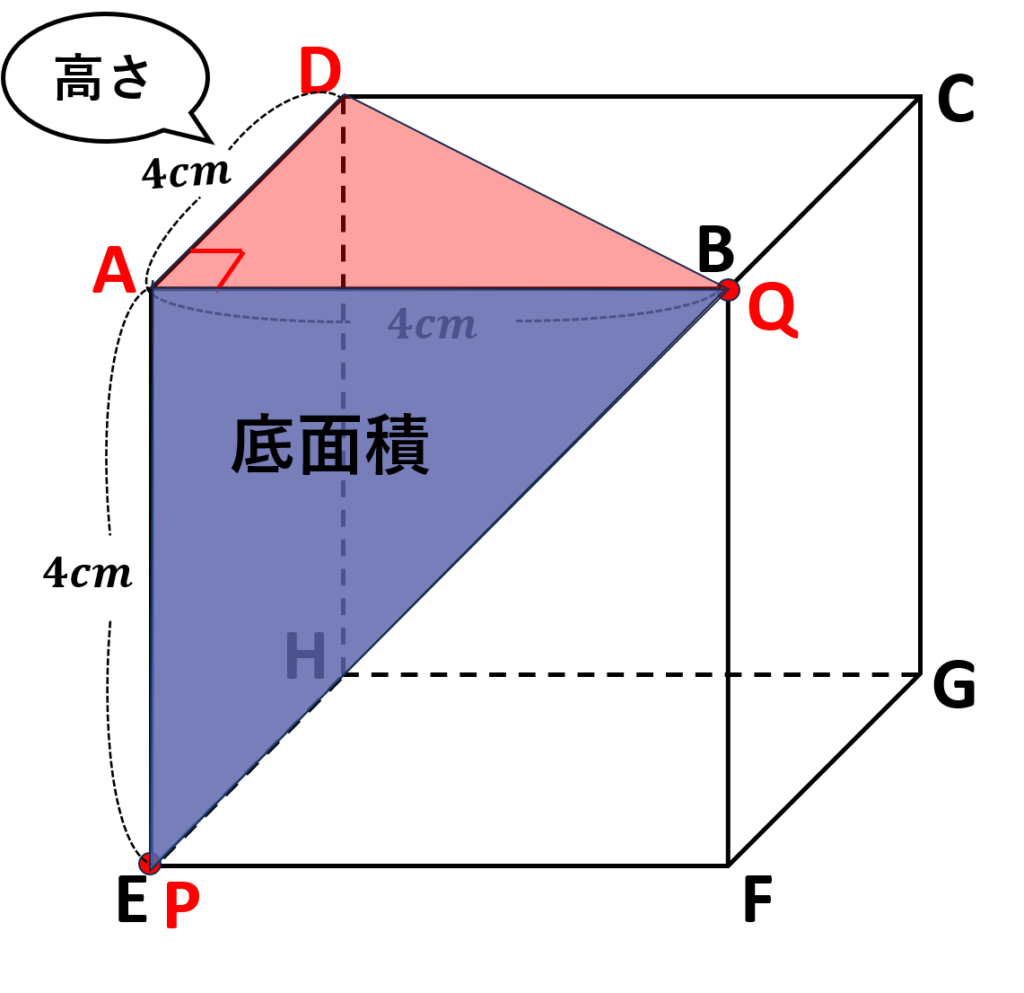
今回はどこを底面にとっても高さは辺の長さと等しくなるので自分が考えやすい形で求めて良い
\(\triangle APQ\)を底面とした場合、高さは\(AD=4cm\)となる
\(\triangle APQ=4\times\cancelto{\color{red}2}{4}\times\displaystyle\frac{1}{\cancelto{\color{red}1}{2}}=8\)
よって三角すい\(APDQ\)の体積は
\(8\times4\times\displaystyle\frac{1}{3}=\displaystyle\frac{32}{3}\)
解答. \(\displaystyle\frac{32}{3}cm^3\)

イ \(2\)点\(P,Q\)が同時に出発してから\(x\)秒後(\(4 < x < 8\))にできる三角形\(APQ\)の面積は何\(cm^2\)か。\(x\)を使った式で表せ。
- \(P,Q\)が\(4~8\)秒の間にいる場所を確認し、三角形\(APQ\)の形を書く
- 辺を\(x\)を使って表す
- 三角形の面積を求める
まずは(\(4 < x < 8\))のとき、点\(P,Q\)がどこにいるか確認しましょう
点\(P\)は点\(A\)を出発して毎秒\(1cm\)で点\(E\)⇒点\(F\)に移動する
⇒\(AE=4cm,EF=4cm\)なので(\(4 < x < 8\))のとき、点\(P\)は辺\(EF\)上にいる
点\(Q\)は点\(C\)を出発して毎秒\(1cm\)で点\(B\)⇒点\(F\)に移動する
⇒\(BC=4cm,BF=4cm\)なので(\(4 < x < 8\))のとき、点\(Q\)は辺\(BF\)上にいる
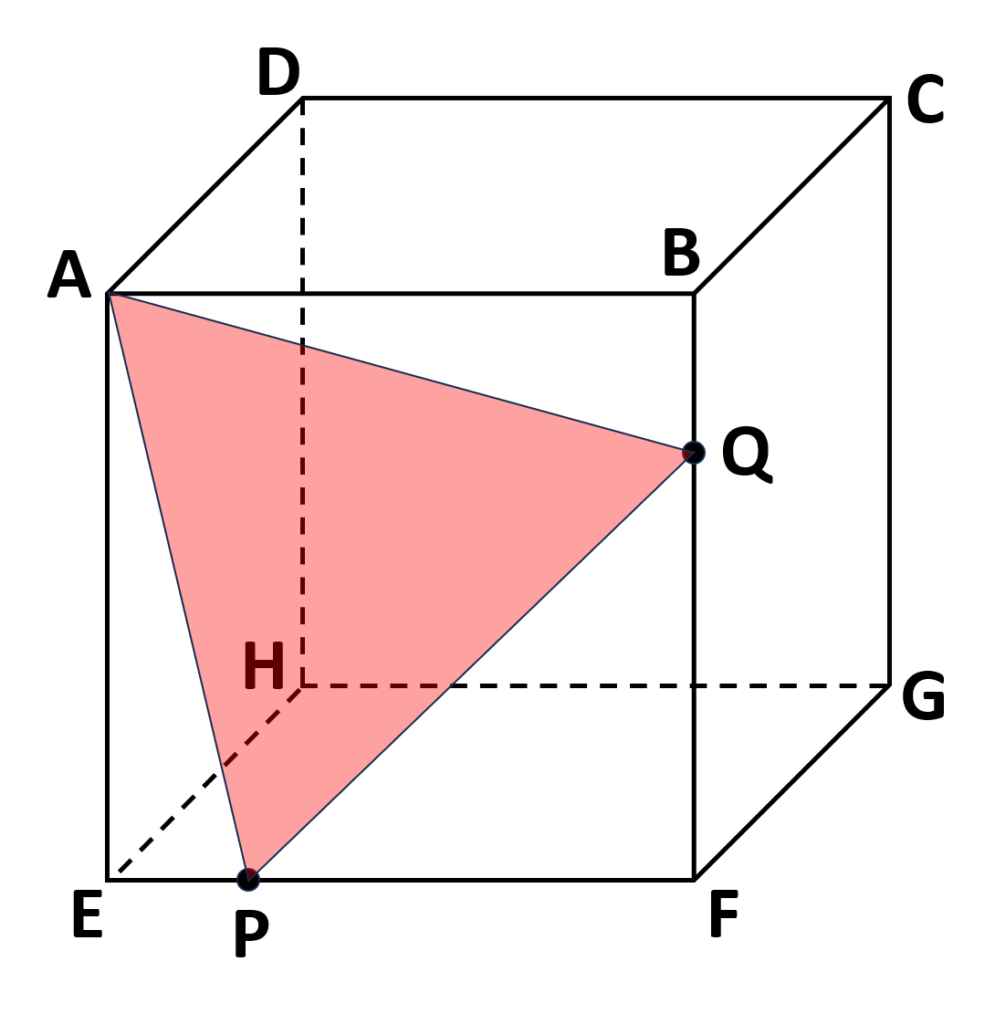

- \(P,Q\)が\(4~8\)秒の間にいる場所を確認し、三角形\(APQ\)の形を書く
- 辺を\(x\)を使って表す
⇒次ココ - 三角形の面積を求める
次は\(x\)を使って\(EP,PF,BQ,QF\)を表していきたい
点\(P\)は点\(A\)を出発して毎秒\(1cm\)で移動するので\(x\)秒後のとき
- \(AE+EP=x\)、\(AE=4cm\)より
\(EP=(x-4)cm\) - \(PF=EF-EP\)より
\(\begin{align}PF&=4-(x-4)\\&=4-x+4\\&=(8-x)cm\end{align}\)
\(※PF=AF-AP=(8-x)\)でも求められる
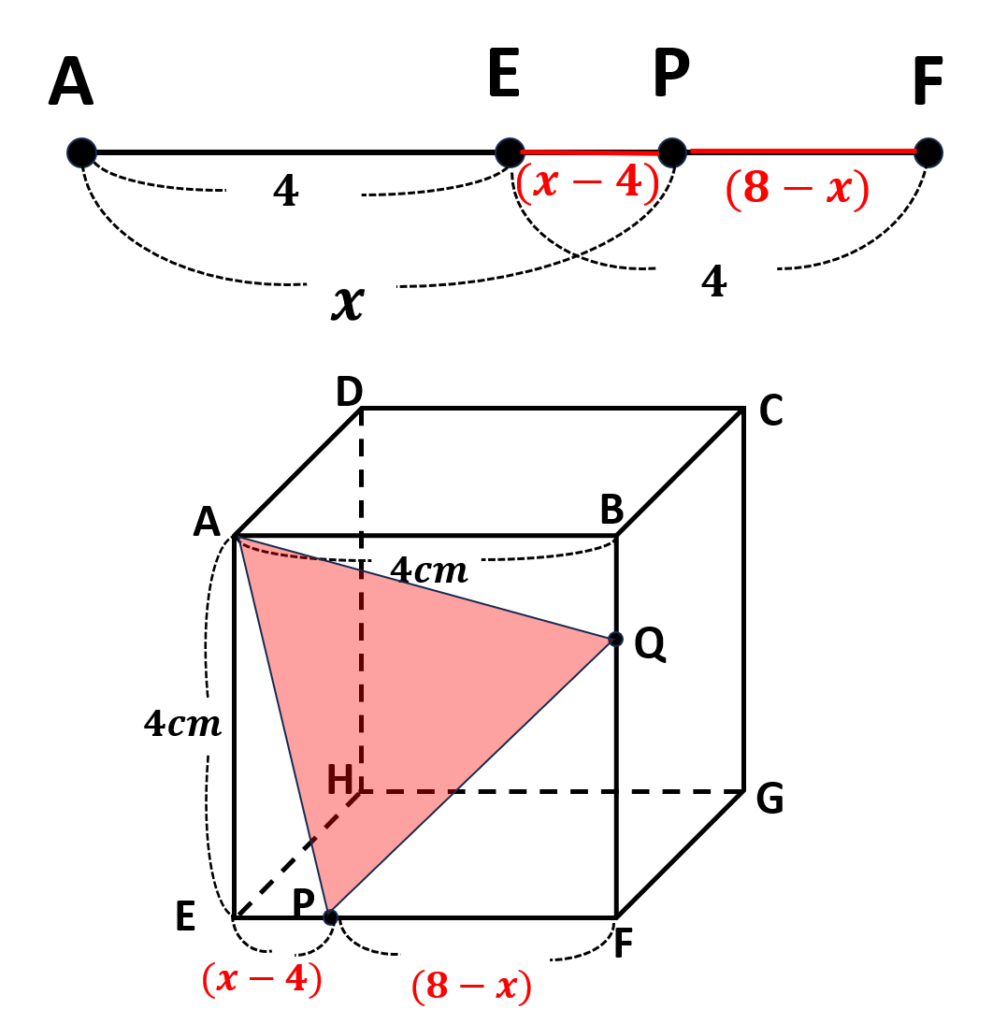

同様に\(BQ,QF\)の長さを\(x\)を用いて表すと
点\(Q\)は点\(C\)を出発して毎秒\(1cm\)で移動するので\(x\)秒後のとき
- \(CB+BQ=x\)、\(CB=4cm\)より
\(BQ=(x-4)cm\) - \(QF=BF-BQ\)より
\(\begin{align}QF&=4-(x-4)\\&=4-x+4\\&=(8-x)cm\end{align}\)
\(※QF=BF-BQ=(8-x)\)でも求められる


- \(P,Q\)が\(4~8\)秒の間にいる場所を確認し、三角形\(APQ\)の形を書く
- 辺を\(x\)を使って表す
- 三角形の面積を求める
⇒次ココ
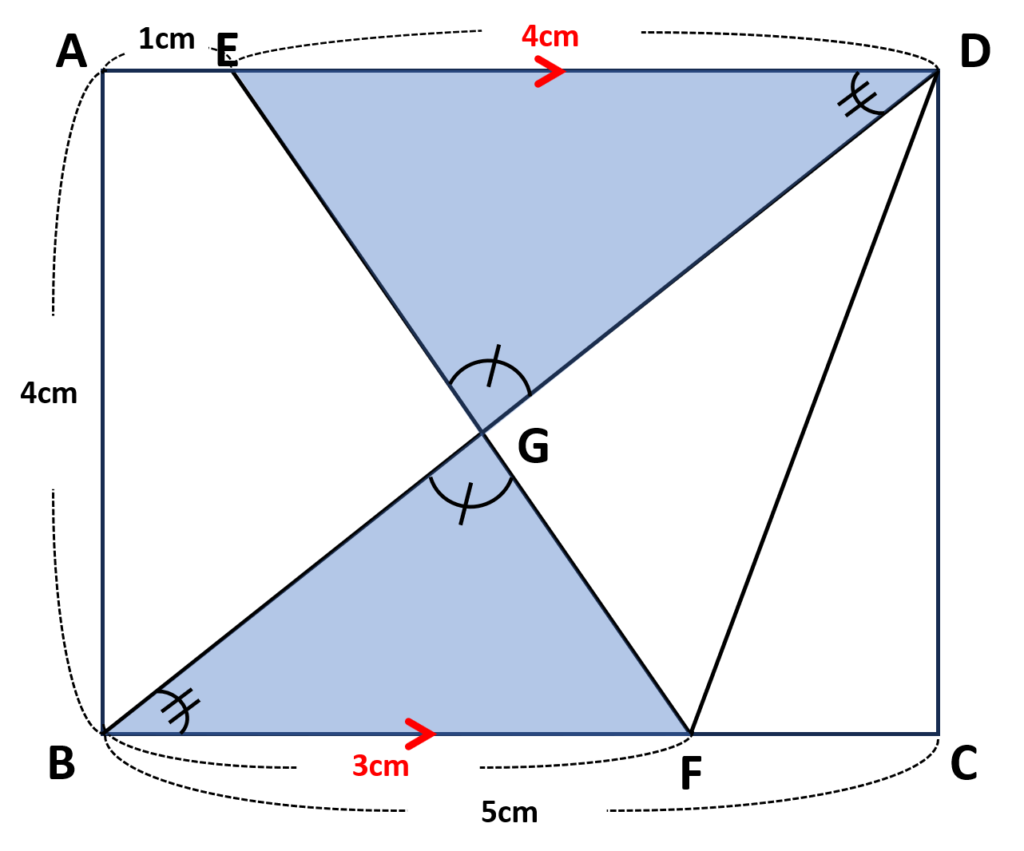
\(\triangle APQ\)の面積を求めていく
四角形\(ABFE\)の中で\(\triangle APQ\)以外の三角形(青塗り部分)をみると、全て直角三角形で面積が求めやすいことがわかる
⇒\(\triangle APQ\)を直接求めるより、四角形\(ABFE\)から不要な三角形(青塗り部分)を引いていく方法の方が良さそう
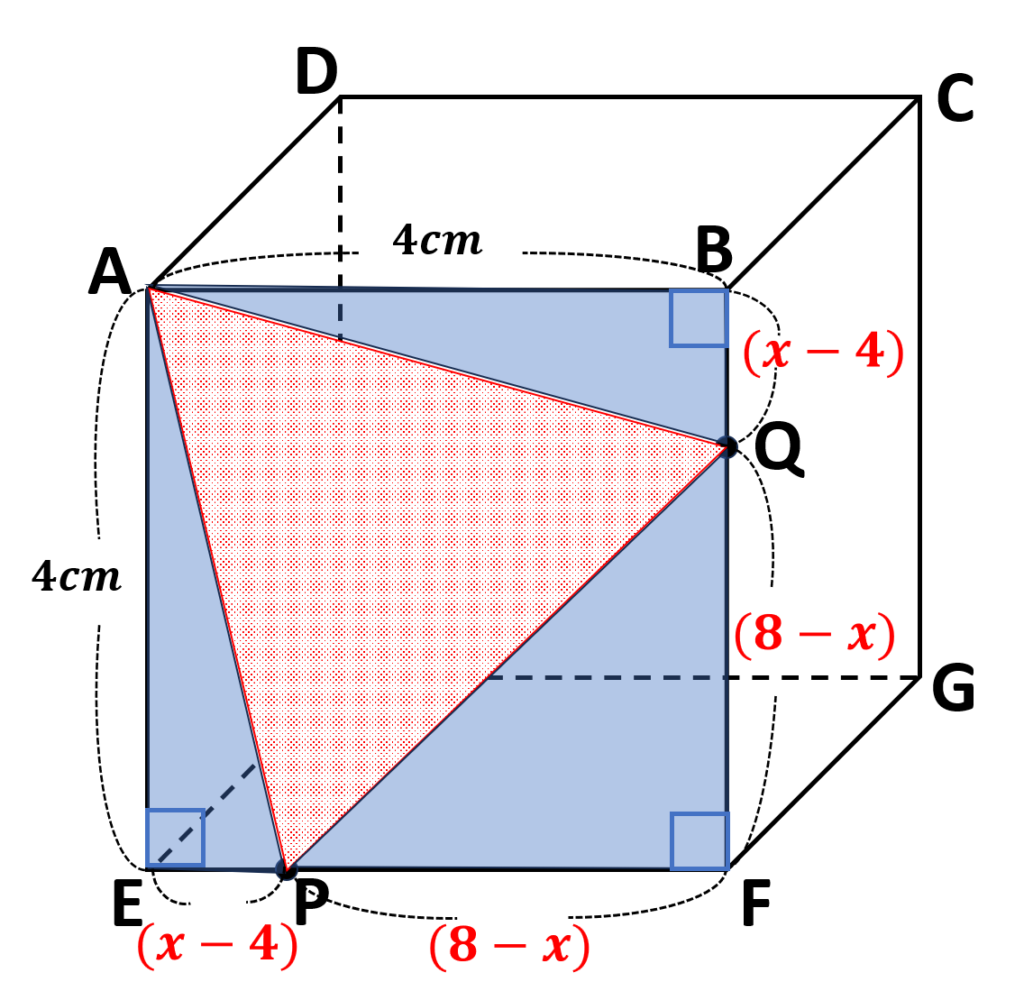

《青塗り部分の三角形の面積》
\(\begin{align}\triangle AEP&=\cancelto{\color{red}2}{4}\times(x-4)\times\displaystyle\frac{1}{\cancelto{\color{red}1}{2}}\\&=2x-8\end{align}\)
\(\triangle ABQ\)も同じなので\(2x-8\)
\(\begin{align}\triangle PQF&=(8-x)\times(8-x)\times\displaystyle\frac{1}{2}\\&=\displaystyle\frac{x^2-16x+64}{2}\\&=\displaystyle\frac{x^2}{2}-8x+32\end{align}\)
よって、青塗り部分の三角形の面積の和は
\(\triangle AEP+\triangle ABQ+\triangle PQF\)
\(\begin{align}&2x-8+2x-8+\displaystyle\frac{x^2}{2}-8x+32\\&=\displaystyle\frac{x^2}{2}-4x+16\end{align}\)
\(\triangle APQ\)の面積は
四角形\(ABFE-(青塗り部分)\)
四角形\(ABFE=4\times4=16\)なので、
\(\begin{align}\triangle APQ&=16-(\displaystyle\frac{x^2}{2}-4x+16)\\&=16-\displaystyle\frac{x^2}{2}+4x-16\\&=-\displaystyle\frac{x^2}{2}+4x\end{align}\)
解答. \((-\displaystyle\frac{x^2}{2}+4x)cm^2\)
ウ \(2\)点\(P,Q\)が同時に出発してから\(x\)秒後(\(4 < x < 8\))にできる三角すい\(APQD\)の体積が、\(2\)点\(P,Q\)が同時に出発してから\(1\)秒後にできる三角すい\(APQD\)の体積と等しくなるときの\(x\)の値はいくらのときか。
- \(1\)秒後の三角すい\(APQD\)の体積を求める
- \(x\)秒後の三角すい\(APQD\)の体積を求める
- ①=②の式より\(x\)を求める
まずは\(2\)点\(P,Q\)が同時に出発してから\(1\)秒後にできる三角すい\(APQD\)の体積を求めていく
- \(1\)秒後の点\(P\)は辺\(AE\)上で、\(AP=1cm\)のところにいる
- \(1\)秒後の点\(Q\)は辺\(BC\)上で、\(CQ=1cm\)のところにいる


底面積を\(ADQ\)とすると、高さは\(AP=1cm\)
よって三角すい\(APQD\)の体積は
\(\begin{align}&底面積(ADQ)\times高さ(AP)\times\displaystyle\frac{1}{3}\\&=4\times\cancelto{\color{red}2}{4}\times\displaystyle\frac{1}{\cancelto{\color{red}1}{2}}\times1\times\displaystyle\frac{1}{3}\\&=\displaystyle\frac{8}{3}\end{align}\)
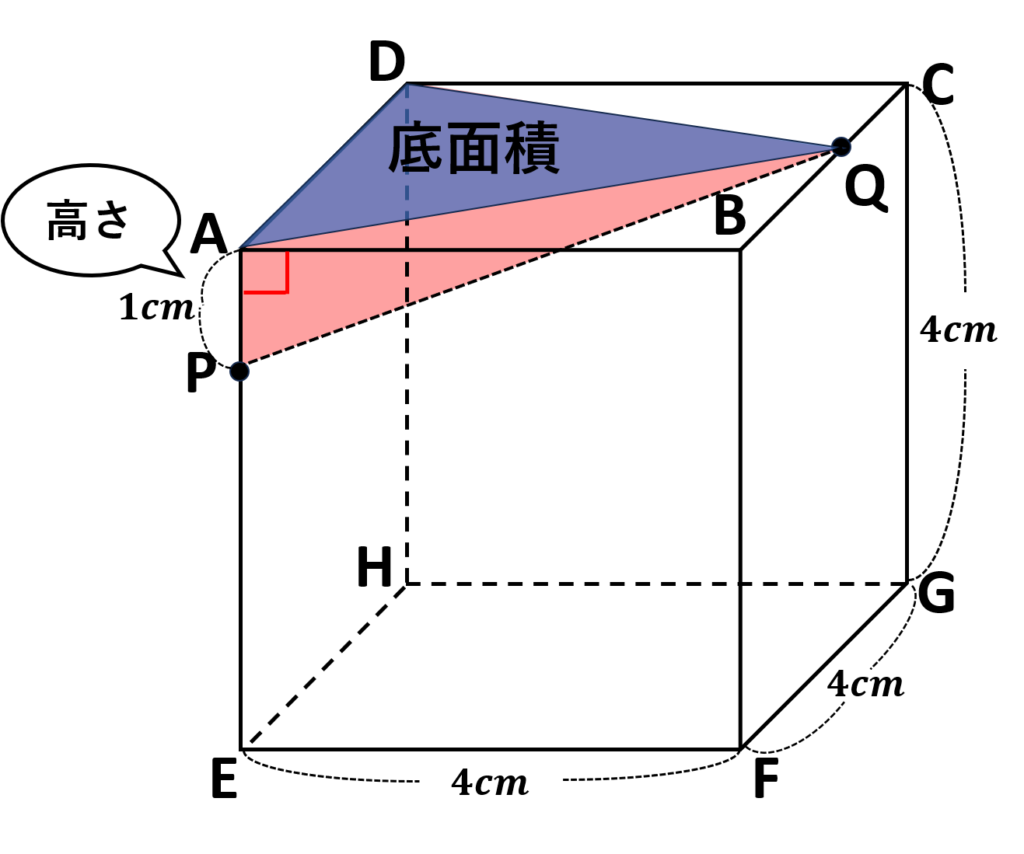

- 立方体なので平面\(ABCD\)と平面\(ABFE\)は垂直
- \(ADQ\)は平面\(ABCD\)上、\(AP\)は平面\(ABFE\)上にいるので
⇒\(ADQ\)と\(AP\)も垂直に交わる
⇒底面積を\(ADQ\)とした場合、高さは\(AP\)の長さと等しくなる
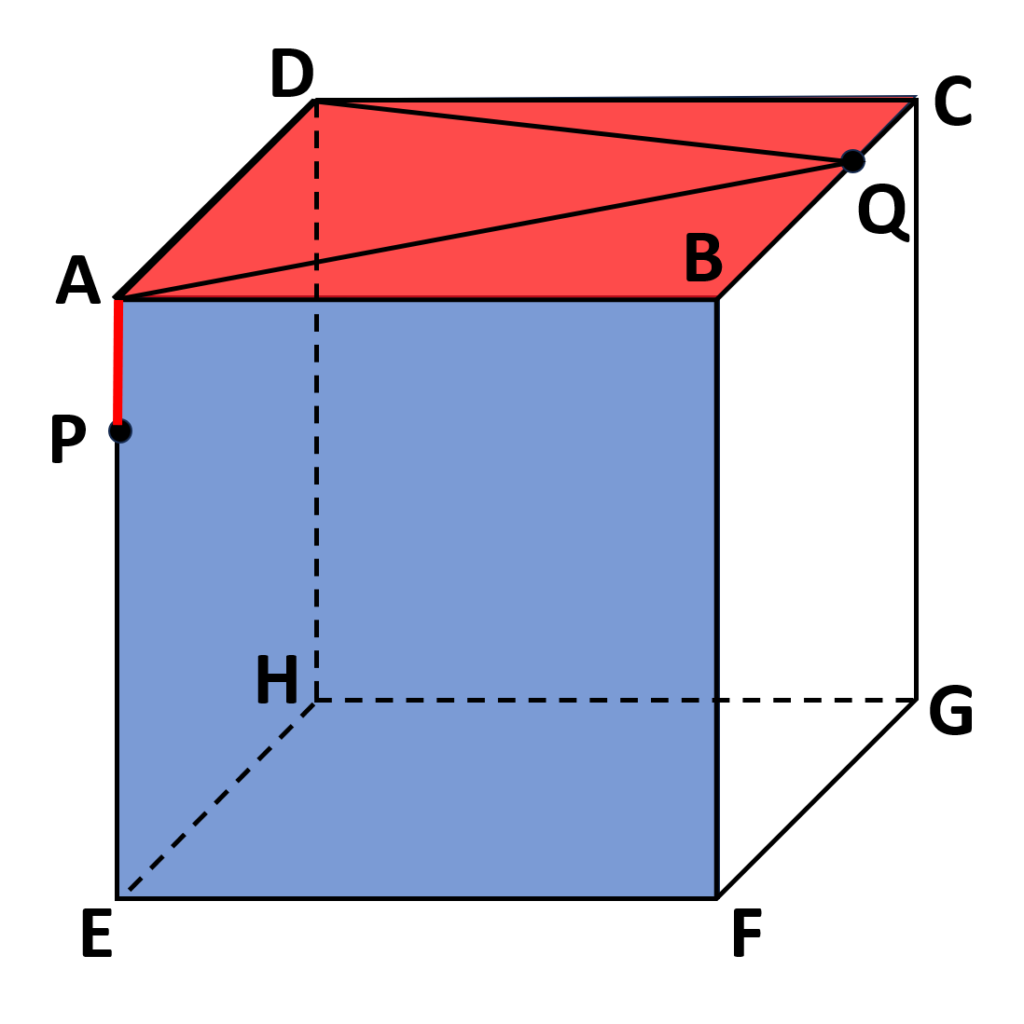

- \(1\)秒後の三角すい\(APQD\)の体積を求める
- \(x\)秒後の三角すい\(APQD\)の体積を求める⇒次ココ
- ①=②の式より\(x\)を求める
次に\(x\)秒後にできる三角すい\(APQD\)の体積を求めていく
問題文より(\(4 < x < 8\))の範囲なので点\(P\)は\(EF\)上、点\(Q\)は\(BF\)上にいることがわかる


底面積を\(APQ\)とすると、点\(A,P,Q\)はいずれも平面\(ABFE\)上にいる
⇒高さは\(AD=4cm\)になる
底面積\(APQ\)は問題イより\((-\displaystyle\frac{x^2}{2}+4x)cm^2\)
よって\(x\)秒後にできる三角すい\(APQD\)は
\((-\displaystyle\frac{x^2}{2}+4x)\times4\times\displaystyle\frac{1}{3}\)
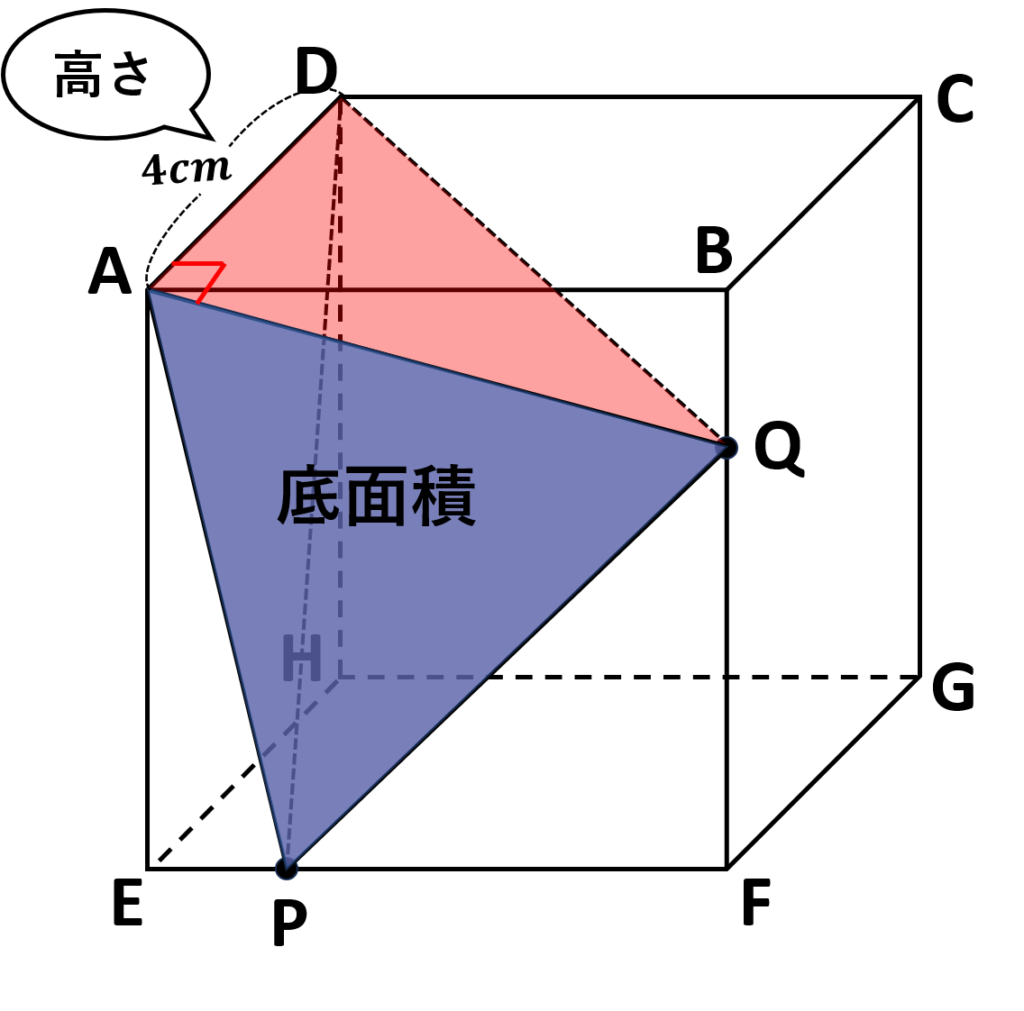

- \(1\)秒後の三角すい\(APQD\)の体積を求める
- \(x\)秒後の三角すい\(APQD\)の体積を求める
- ①=②の式より\(x\)を求める⇒次ココ
\(1\)秒後、\(x\)秒後の三角すい\(APQD\)の体積が等しいときの\(x\)を求めたいので
\((x秒後の体積)=(1秒後の体積)\)の式を解いて\(x\)の値を求める
\((-\displaystyle\frac{x^2}{2}+4x)\times4\times\displaystyle\frac{1}{\cancelto{\color{red}1}{3}}=\displaystyle\frac{8}{\cancelto{\color{red}1}{3}}\)
\((-\displaystyle\frac{x^2}{2}+4x)\times\cancelto{\color{red}1}{4}=\cancelto{\color{red}2}{8}\)
\(-\displaystyle\frac{x^2}{2}+4x=2\)
両辺に\(2\)をかけて分母を払うと、
\(\begin{align}&-x^2+8x=4\\&x^2-8x=-4\\&x^2-8x+4=0\end{align}\)
解の公式より
\(\begin{align}x&=-(-4)\pm\sqrt{4^2-1\times4}\\x&=4\pm\sqrt{16-4}\\x&=4\pm\sqrt{12}\end{align}\)
\(x=4\pm2\sqrt{3}\)
\(x\)は\(4 < x < 8\)なので
\(x=4+2\sqrt{3}\)
解答. \(x=4+2\sqrt{3}\)



\(x\)の範囲を確認するのを忘れずに!
\(ax^2+bx+c=0\)の\(b\)が偶数の場合、
\(b’=\displaystyle\frac{b}{2}\)とすると
\(x=\displaystyle\frac{-b’\pm\sqrt{(b’)^2-ac}}{a}\)



\(b\)が偶数のときはこの計算の方が早いので使っていこう!
図形上を動く問題は
- \(x\)がどこの長さを表しているか
- \(x\)の範囲は決められているか
をしっかり確認する
面積を問われた場合は
- 直接求める
- 図形を分割する
- 大きい図形から余分な部分を引く
のいずれかの方法で考えましょう!
垂直に交わる辺などを利用すると簡単に計算できます
体積の場合は
- 底面積をどこにすれば簡単に求められるか
を考えることがポイントです!
垂直に交わる辺を利用する、同じ平面上にある三角形を底面積にすると計算しやすいです
問題5
(1)
\(\triangle ACH\unicode[sans-serif]{x223D}\triangle GBH\)を証明せよ。
円と図形の組み合わせは
- 円周角や図形の性質を利用
- 同じ角をどんどん見つけていく
ことが大切!

- 証明する三角形を確認
- 同じ角や辺を見つけていく
- 相似条件に当てはまるものを利用する
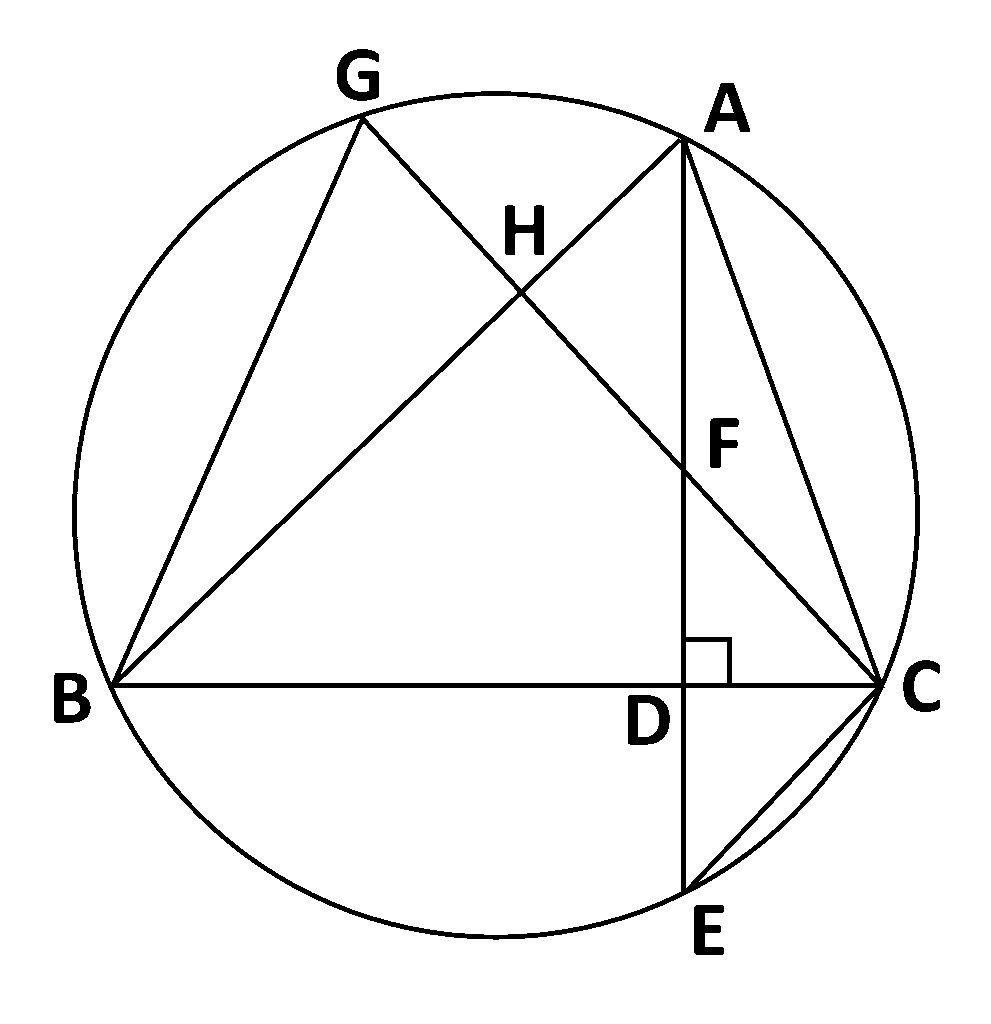
まずは証明する三角形\(\triangle ACH,\triangle GBH\)を確認しましょう


次に同じ角や辺を図形の性質より見つけていきましょう
- 対頂角より\(\angle{AHC}=\angle{GHB}\)
- 弧\(BC\)の円周角より\(\angle{HAC}=\angle{HGB}\)
- 弧\(GA\)の円周角より\(\angle{ACH}=\angle{GBH}\)
\(2\)組の角がそれぞれ等しいので
\(\therefore\triangle ACH\unicode[sans-serif]{x223D}\triangle GBH\)
\(\angle{AHC}=\angle{GHB}\)


\(\angle{HAC}=\angle{HGB}\)
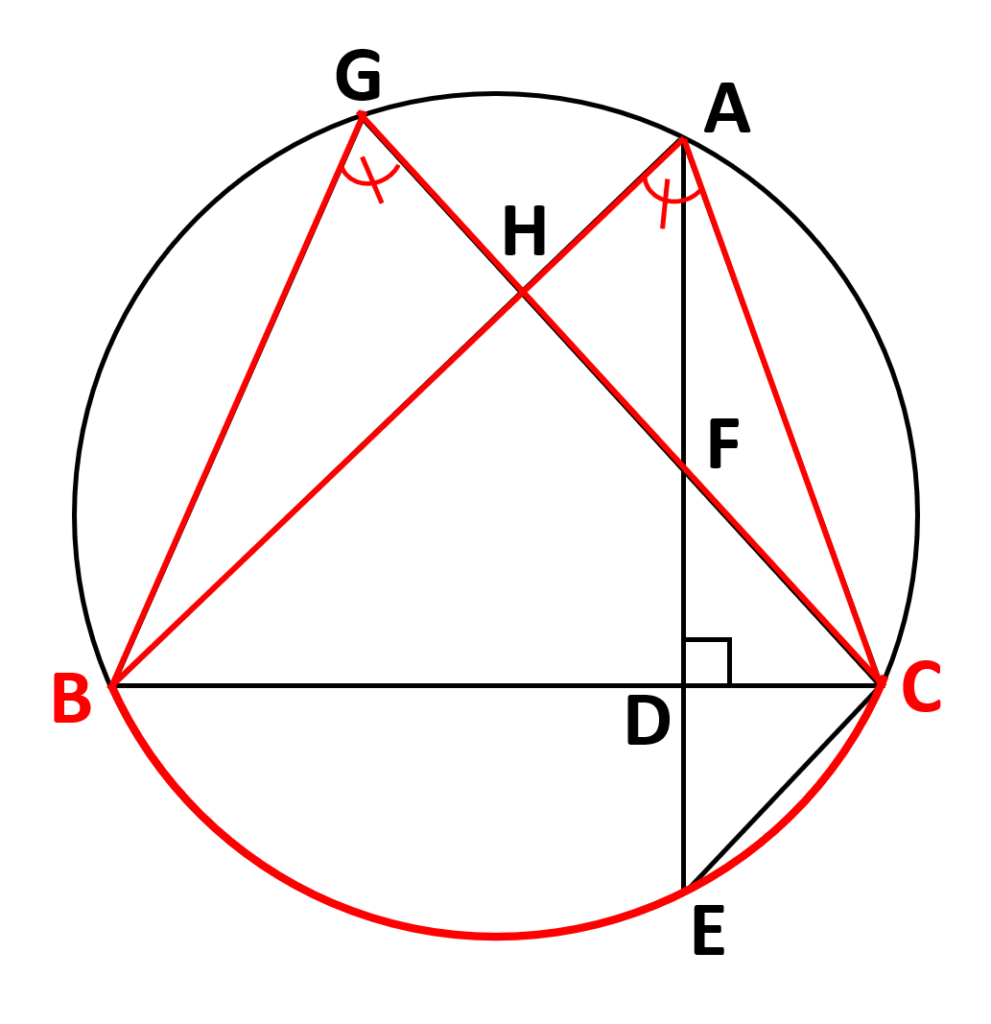

\(\angle{ACH}=\angle{GBH}\)


(2)
\(\triangle ABF\equiv\triangle ABG\)であることを証明せよ。
- 証明する三角形を確認
- 同じ角や辺を見つけていく
- 合同条件に当てはまるものを利用する
証明する三角形を確認していく
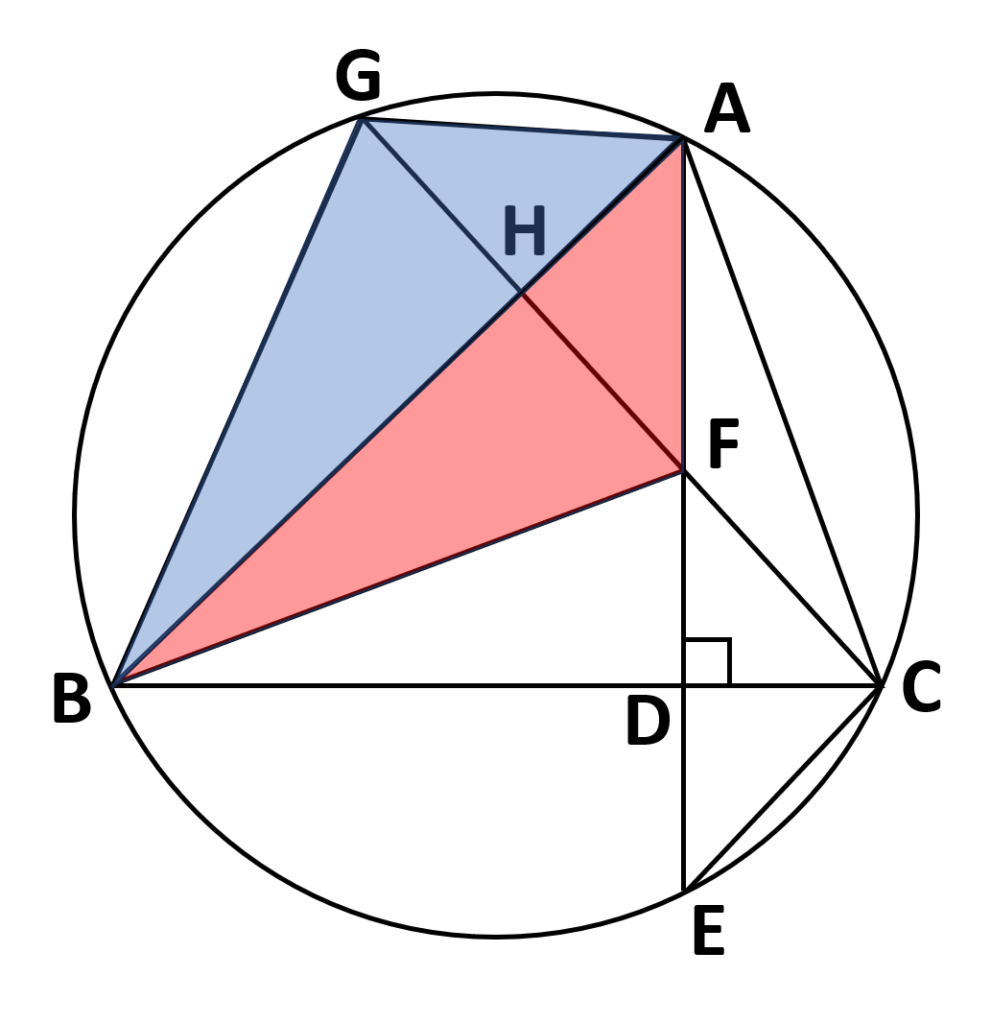

(1)同様、三角形や図形の性質から同じ角度や辺を見つけていく



証明する三角形と遠い角度でも考えていくことが大切!
気付いたら繋がっていくことが多いので、わかるとこはどんどん埋めていこう!
問題文より\(CE=CF\)という条件があるので、そこから考えていく
- \(CE=CF\)より\(\triangle CEF\)は二等辺三角形
⇒\(\angle{CFE}=\angle{CEF}\) - \(CD\)と\(EF\)は垂直に交わっている
⇒\(CD\)は頂角\(\angle{FCE}\)を二等分する
⇒\(\angle{FCD}=\angle{ECD}\)
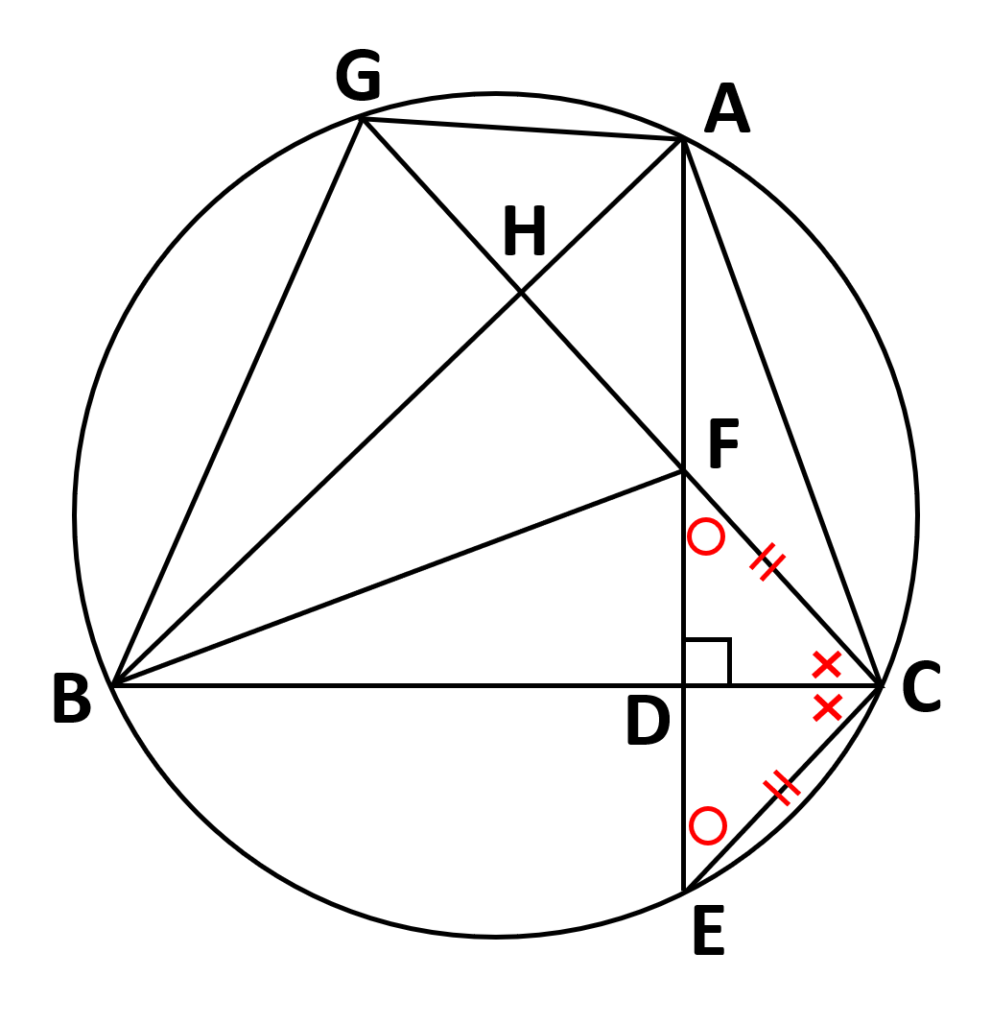

次に先ほど目印をつけた角度と同じ角度に同じ目印をつけていく
まず「×印」と同じ角度について考えていく
×印は\(\angle{FCD}と\angle{ECD}\)
\(\angle{FCD}\)の円周角について考えると
- \(\angle{FCD}\)は\(\stackrel{\huge\frown}{GB}\)の円周角なので
⇒\(\angle{FCD}=\angle{GAB}\)


同様に\(\angle{ECD}\)の円周角について考えると
- \(\angle{ECD}\)は\(\stackrel{\huge\frown}{BE}\)の円周角なので
⇒\(\angle{ECD}=\angle{BAE}\)


よって
- \(\angle{GAB}=\angle{FAB}\)
が成り立つ
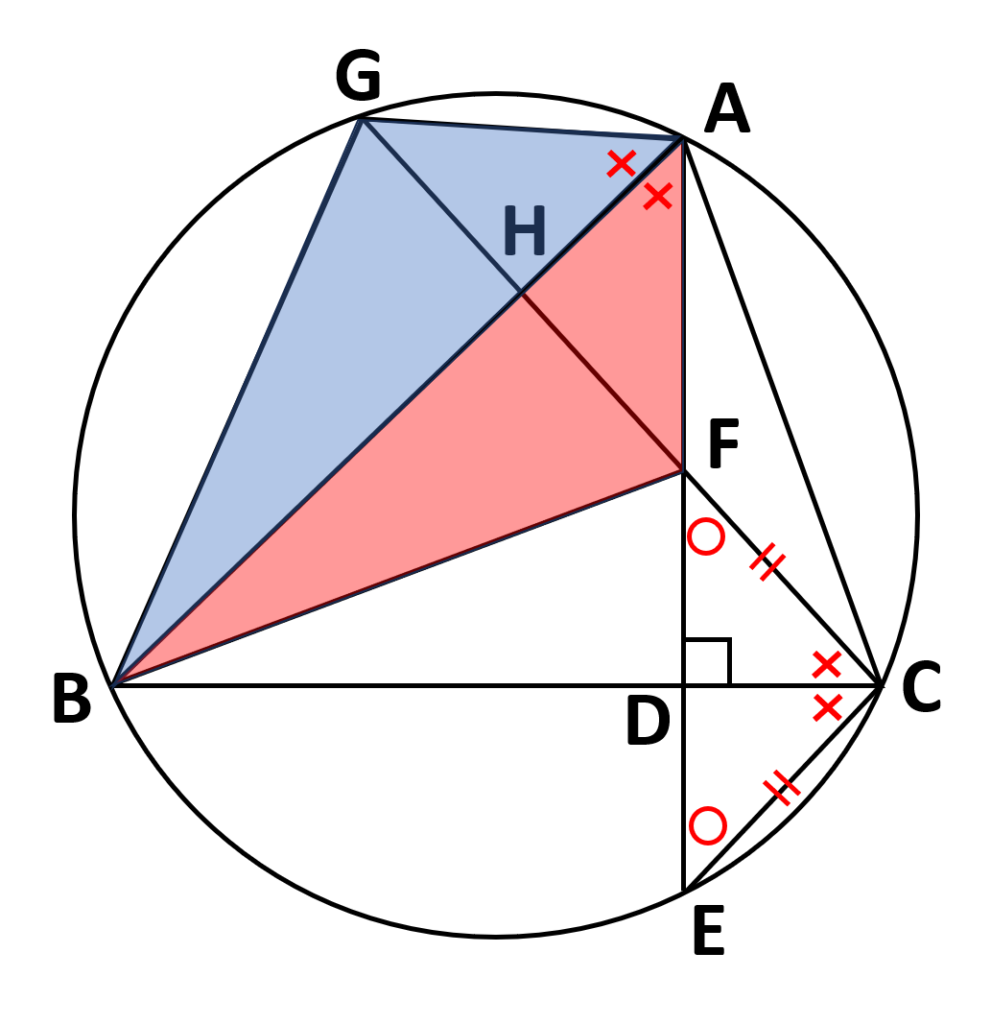

次に「〇印」と同じ角度について考えていく
〇印は\(\angle{CFD}と\angle{CED}\)
\(\angle{CFD}\)について考えると
- 対頂角より\(\angle{CFD}=\angle{AFG}\)
が成り立つ
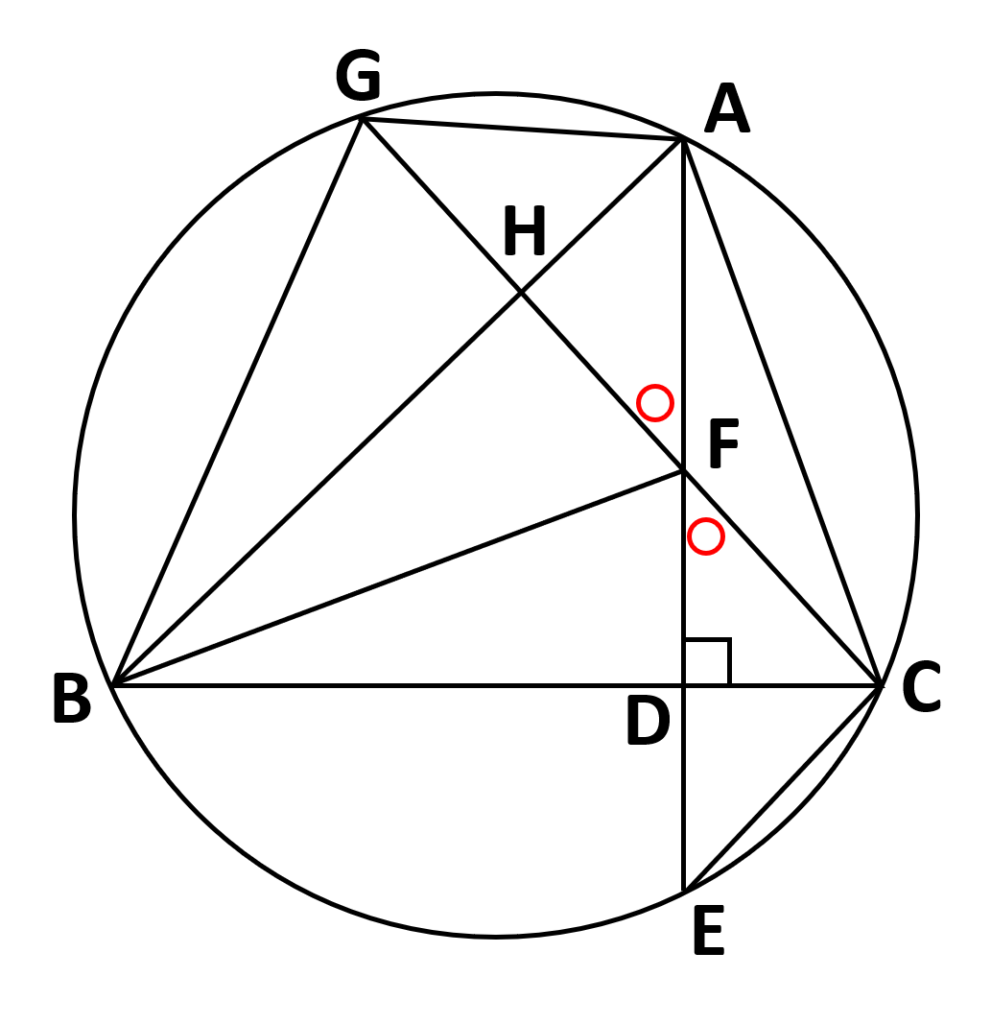

次に\(\angle{CED}\)について考えると
- \(\angle{CED}\)は\(\stackrel{\huge\frown}{AC}\)の円周角なので
\(\angle{CED}=\angle{CGA}=\angle{CBA}\)
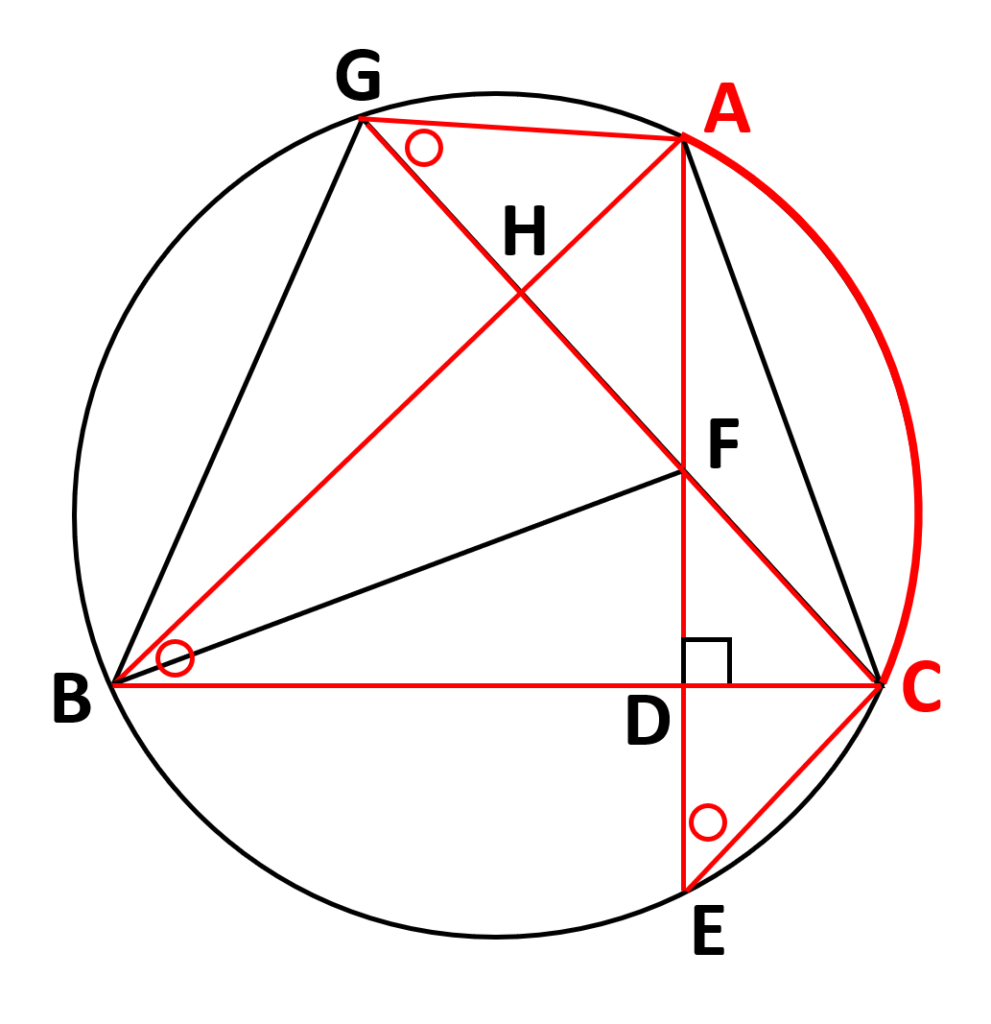

新たにわかった情報を図形に書き込むと、
- \(\angle{AFG}=\angle{AGF}\)より
\(\triangle AGF\)は二等辺三角形であることがわかる
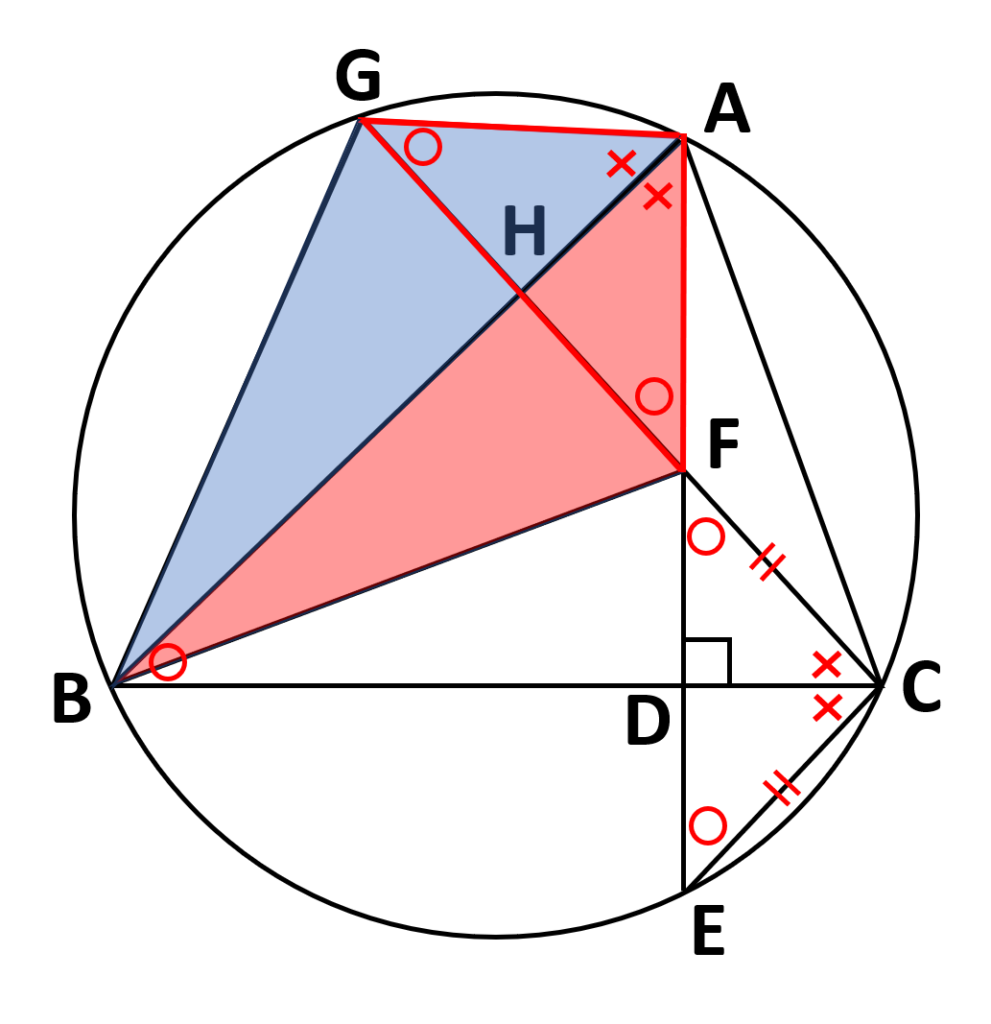

\(\triangle AGF\)が二等辺三角形より
- \(AG=AF\)
- \(AH\)は\(GF\)を垂直二等分線する
が成り立つ
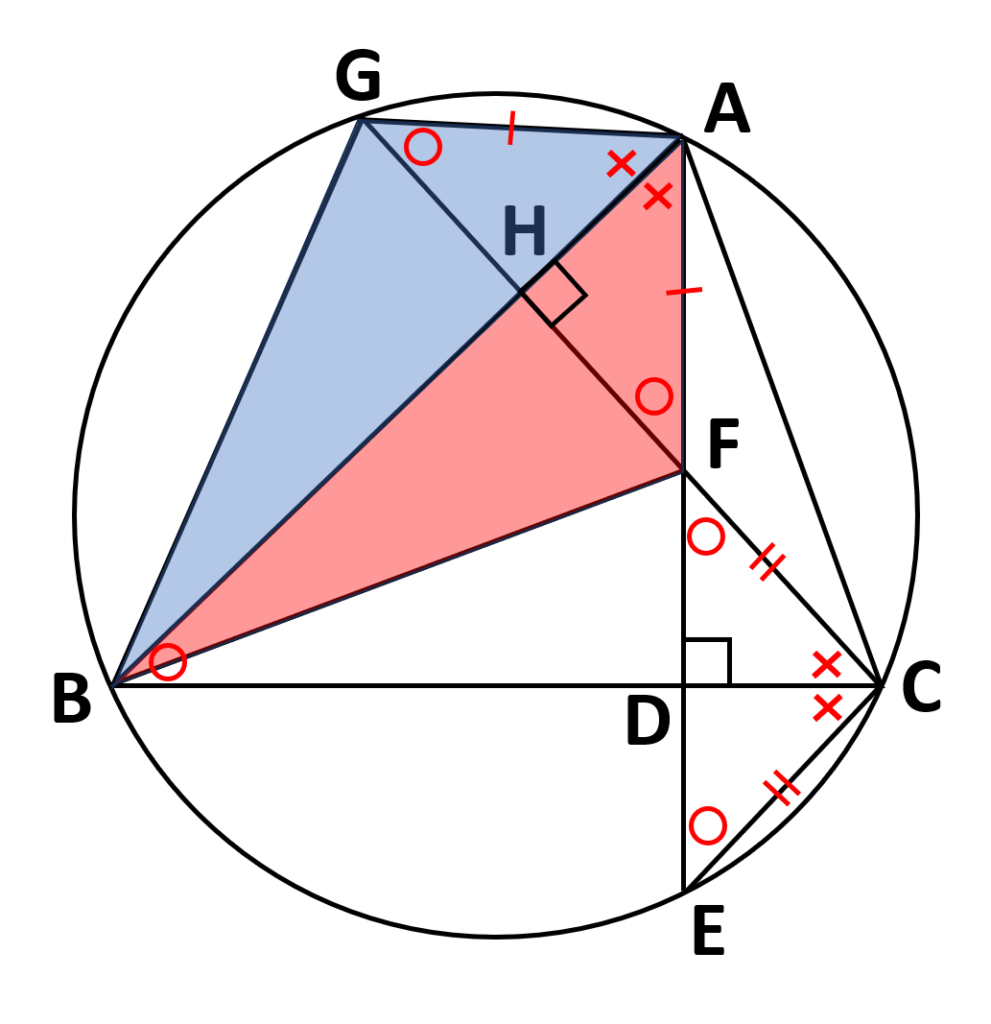

証明する三角形を確認すると、
- \(\angle{BAF}=\angle{BAG}\)
- \(AF=AG\)
- \(AB\)は共通
二辺とその間の角が等しいので
\(\therefore\triangle ABF\equiv\triangle ABG\)